从0开始学习PBRT#
概况
- 过一遍必要的知识点尽量记录自己的理解和推导记录有用的资料/资源
- 把图形学捡起来做一个小小渲染器
- 其实有点觉得从0直接看pbrt能更好学习图形学原理因为能从最底层的结构一步步搭建程序且不用折腾市面上的图形api当然一般都是从图形api开始因为更容易出结果
- 这个书是参考书性质无基础的话需要颠来倒去看很多知识点都是一环套一环每个小问题都可能引出一堆问题
- 需要学习研究大量各方面知识包括数学物理编程等等需要看各种相关论文和书籍
- 要吃透所有知识点很困难需要反复学习思考是个长期过程有的细节要敢于暂时忽略
需要的基本知识
线性代数
微积分
概率
如果有图形学基础会比较舒服
可以先大致看看书,然后搞一下初始代码。
目前的代码
useyourfeelings/cranks-renderer.git
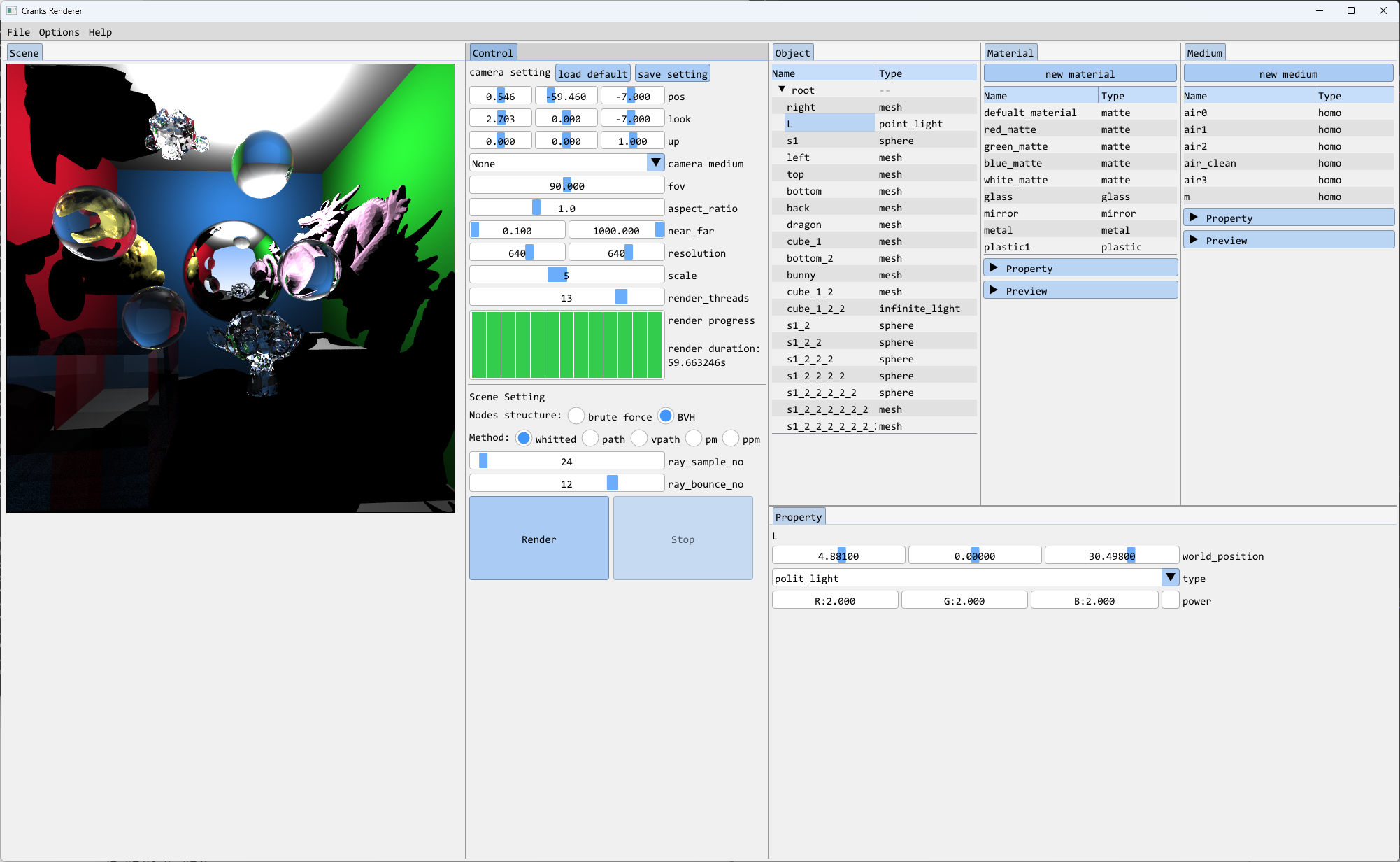
image#
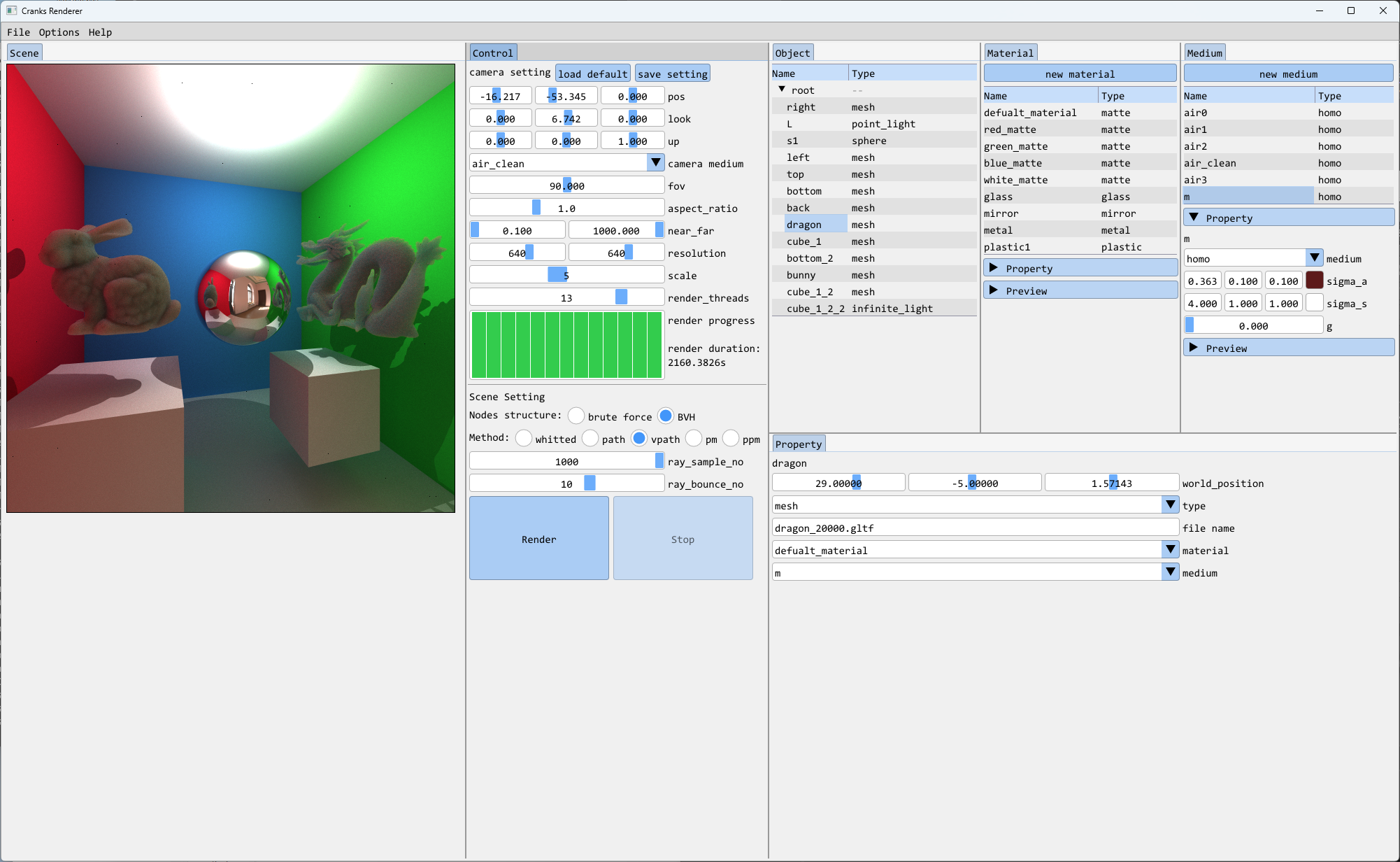
image#

image#

image#

image#

image#

image#

image#

image#
起环境#
编译成功运行可看到imgui的demo窗口。
把我们自己的界面和逻辑写在别的文件里管理好。最后在main里驱动即可。
到此gui基础框架起好了。
我的代码进程:
基本几何
矩阵变换
透视相机
球体
球体与光交互
PointLight
RandomSampler
WhittedIntegrator
Lambertian bxdf
matte/玻璃/镜面材质
到这里可以出图了
然后
错误处理
多线程渲染
PathIntegrator 路径追踪
mipmap / hdr / 环境光 / infinite light
三角形 / mesh / 简单glTF加载
BBox / BVH
微小面bxdf
完善gui(物体的crud / material的crud / 场景存取)
简单texture
kd-tree
photon mapping 光子映射
优化 / 内存池
体渲染 / 次表面
我是抄到大概了解了WhittedIntegrator的流程以后开始出图。
pbrt的代码我比较懒,都没编过没跑过。就硬看书和代码,再用自己的代码一点点调起来。
1 介绍#
1.2 PHOTOREALISTIC RENDERING AND THE RAY-TRACING ALGORITHM#
1.2.2#
计算ray和面的交点
1.2.3 光的分布#
严格的点光源实际是不存在的。基于物理的光照一般是基于面光源。
1.2.4 阴影#
1.2.5 表面散射#
入射光如何散射出去
这样有了光,方向,表面和材质。就可以算点上的光了。
radiance 辐射率
其他各种df
1.2.6 间接光#
原始的光源打到物体上反射出去,又可以看作是一个光源。
间接怎么理解。即除了本身的发光外,所有光源打过来的光,包括直接光源和其他物体反射过来的光。
对于不是极为简单的场景,实际光源可以说是无数个。硬算肯定是不行的。要做简化。
最初的Whitted算法。对一个点只考虑一些重要的方向进来的光,比如镜面方向和折射方向。大大的简化。
在这基础上可以改进。比如多取一些与镜面方向相近的光,可得到glossy效果。
1.2.7 光的传播#
两种影响。吸收和散射(发散到不同的方向)
1.3 pbrt系统概览#
介绍代码结构
1.4 并行化#
多线程细节非常多,可以追究到硬件/cpu等层面。
看c++的lambda相关
看c++的thread相关
看c++的memory模型。new/placement new等。
线程里可以读公共数据,尽量不要去写。
线程里不要频繁动态分配内存,不要频繁起std::vector之类。
分配内存用内存池。
有些数据结构需要手写,可比std的更实用高效。
把场景平均分块给多线程计算。可能有的部分更复杂,造成拖慢整体进度。需要实现让完成任务的线程自动去分担没完成的任务,不让cpu空闲。
pbrt的内存池MemoryArena比较简单直接
定一个block大小比如256k。每次实际分配的大小为256k的整数倍,为一个大块。
分配内存要使用带对齐的api。
有一个free链表存可用的大块
有一个busy链表存正在使用的大块
有一个独立的当前大块
申请时先看当前大块剩余空间是否足够。
足够直接用。
不足的话当前大块进busy表,在free表中查找是否有空间足够的大块。
找到就用
找不到就必须新分配内存
只支持单线程。在每个线程起唯一一个实例。
每个线程会进行大量循环操作,每次的操作是独立线性的。
每次循环之前清空block(只是逻辑清空,都进入free表,并不实际free内存)。
线程结束时调用实际的free。
总体只需申请1次循环中操作锁需要的内存,后续的循环大都是复用内存。
2 geometry 和 transformation#
确定坐标系
定义基本的向量/点/ray之类。
空间变换。各种矩阵操作。四元数暂时不用实现。
坐标系#
分左手/右手。zUp/yUp。
坐标系会影响一些变换。比如lookat。
2.5 ray#
\({\Large r(t)=o+td}\)
2.5.1 RayDifferential#
RayDifferential这个类在初期用不到。它在第10.1章用于Texture的相关计算。
见PerspectiveCamera::GenerateRayDifferential
2.7 transformation#
各种矩阵变换
齐次坐标
经典的mvp矩阵
local space 先有local坐标,即模型自己的坐标,建模时的坐标。
local坐标C
world space 我们创造各种程序、各种世界,每个世界都有各自的坐标系/原点。 把模型导入一个世界,就必须指定模型在这个世界中的位置、方向。 也就是把模型从原点做矩阵变换。经过平移/旋转等等放到世界里。
MODEL矩阵M
把坐标乘上M得到 M*C。world space里的坐标
view space 观察空间/相机空间 任何一个画面一定是基于一个观察位置和观察方向。或者比如说基于固定的相机或者眼睛。
此时坐标变成 V*M*C
clip space
P*V*M*C。lookat矩阵#
https://learnopengl.com/Getting-started/Camera
坐标系是上z 右x 前y
\(L = dot(T - C, U)\)
\(L = Ux(Tx - Cx) + Uy(Ty - Cy) + Uz(Tz - Cz) = dot(U, T) - dot(U, C)\)
这个距离就是最终的z值。同理可算出最终的x,y。
\(\left\{\begin{matrix} x=dot(R, T)-dot(R, C)\\ y=dot(D, T)-dot(D, C)\\ z=dot(U, T)-dot(U, C) \end{matrix}\right.\)
还是对于z,凑一个矩阵相乘。
\(\begin{bmatrix} Ux &Uy &Uz & 0 \end{bmatrix} \times \begin{bmatrix} 1& 0& 0 &-Cx \\ 0& 1& 0&-Cy \\ 0& 0& 1&-Cz \\ 0& 0& 0&1 \end{bmatrix}\)
其他两轴一样处理,最后得到lookat矩阵。
\(\begin{bmatrix} Rx& Ry& Rz& 0 \\ Dx& Dy& Dz& 0 \\ Ux& Uy& Uz& 0 \\ 0& 0& 0&1 \end{bmatrix} \times \begin{bmatrix} 1& 0& 0 &-Cx \\ 0& 1& 0&-Cy \\ 0& 0& 1&-Cz \\ 0& 0& 0&1 \end{bmatrix}\)
可以接着看看第六章Camera
2.10 相交#
SurfaceInteraction的一些解释
面的normal问题#
3 形状#
3.1 基本接口#
shape基类
3.1.1 bbox#
AABB
3.1.2 光与bbox求交#
An Efficient and Robust Ray–Box Intersection Algorithm
某个垂直于x轴的平面
\(x=X_{1}\)
光打到某点的坐标
\(O+tD\)
那么光打到平面,只看x轴,有
\(O_{x} + tD_{x} = X_{1}\)
可求得
\({\Large t=\frac{X_{1}-O_{x}}{D_{x}}}\)
那么对两个对立面,按光的方向,可求得tmin和tmax。
这样子依次算三个轴,如果t有交集就是相交。
可以把\({\Large \frac{1}{D}}\)在三个轴上的值提出来先算好,再做乘法,更快。一般乘法会快一些。
可以把\({\Large \frac{1}{D}}\)提到求交函数外面,这样同一个光与大量bbox求交时,可以提速。
- 特殊情况光在某个轴的方向为0。除的话为无穷大。而IEEE又有0和-0之分,除出来是正无穷和负无穷。会造成检测失败。不过我在VS2022里貌似没试出来,除0和-1都得到inf,并没有-inf。可能方法不对,暂忽略。最终应该再区分一下\(D\)的正负方向,按需交换tmin和tmax。
错误处理见3.9.2
3.2 球体#
球体与射线的交点
// 设s为球面上的交点
// 对于球 ||s - c||=r
// 对于ray s = o + dt
// ||o + dt - c|| = r
// c = 0, 0, 0
// (o + dt) dot (o + dt) = r*r 自己点乘自己是长度的平方
// 算出来得到 oo + 2tod + ttdd = rr
// 解t的一元二次方程
// a = dd
// b = 2od
// c = oo - rr
// att + bt + c = 0
解出t。即可算出交点。
从球坐标看
\(x = r sin(θ) cos(φ)\)\(y = r sin(θ) sin(φ)\)\(z = r cos(θ)\)
y / x = tan(φ)
可以算出交点的φ = atan(y / x)
phimax默认值是360
3.6 三角形mesh#
glTF模型#
3.9 error处理#
浮点数计算是有误差的。需要学习数值计算相关。
[Accuracy and Stability of Numerical Algorithms]可以先跳过,出问题后再回来看。
3.9.1 浮点数计算#
浮点数的表示#
https://en.wikipedia.org/wiki/Single-precision_floating-point_format
浮点数是经过巧妙设计的。可以发展出一套方法,得到令人吃惊的小误差。
要知道IEEE浮点数和bit数据如何相互转换
比如1的最终bit数据是0x3f800000
0???
0 00000000 00000000000000000000000
1
0 01111111 (1.)00000000000000000000000 (1) * pow(2, 0)
0b0111111100000000000000000000000 = 0x3f800000
2
0 10000000 (1.)00000000000000000000000 (1) * pow(2, 1)
3
0 10000000 (1.)10000000000000000000000 (1 + 1/2) * pow(2, 1)
4
0 10000001 (1.)00000000000000000000000 (1) * pow(2, 2)
5
0 10000001 (1.)01000000000000000000000 (1 + 1/2*2) * pow(2, 2)
std::numeric_limits<float>::epsilon()的值https://en.wikipedia.org/wiki/Machine_epsilon
算术计算#
就是说它保证了绝对的稳定性和极高的准确性。
\({\large a \oplus b = round(a+b)}\)
\({\large a \ominus b = round(a -b)}\)
\({\large a \otimes b = round(a * b)}\)
\({\large a \oslash b = round(a /b)}\)
\({\large sqrt(a) = round(\sqrt a)}\)
[Accuracy and Stability of Numerical Algorithms]定理2.2给出也就是说任意x一定可以rounding到一个相对误差在\(\frac{ulp}{2}\)内的浮点数。
-----|---------------x--------|--------------------|------------
t1E tE t2E t3E
| 远 | 近 |
rounding的操作性质,离哪个更近就往哪边靠,决定了\(|fl(x)-x|\le\frac{t2E - t1E}{2}\)。
而\(t2E - t1E=ulpE\)
所以有 \(|fl(x) - x| \le \frac{ulp E} {2}\)
两边除以\(x=tE\)
\(|(fl(x) - x) / x| \le \frac{ulp}{2t}\)
因为\(t \ge1\),所以右边\(\le \frac{ulp}{2}\)。
即右边的最大值是\(\frac{ulp}{2}\),而左边小于等于右边,所以左边一定\(\le\frac{ulp}{2}\)。
即得到了相对误差的上限。
\(x(1 \pm e)\)是一个标准模型。
也可以用别的模型比如,\(fl(x)=\frac{x}{1 \pm e}\)也成立。
\({\large a\oplus b = round(a + b)}\)
最终会落在
\([(a + b)(1−e), (a + b)(1+e)]\)
其中\(e\)一定小于等于\(\frac{ulp}{2}\)。见上面的证明。
std::numeric_limits<float>::epsilon() / 2误差的传导#
在IEEE标准的基础上,可以推理出一套方法来分析和限定浮点数计算中的误差。
相对误差和绝对误差
绝对误差就是round过后的结果与正确结果的差的绝对值。
相对误差就是绝对误差占正确值的百分比。
以四个浮点数相加为例
\({\large (((a ⊕ b) ⊕ c) ⊕ d)}\)
\({\large \subset (((a+b)(1 \pm e) +c)(1 \pm e) + d)(1 \pm e) }\)
\({\large = (a+b)(1±e)^{3} + c(1±e)^2 + d(1±e)}\)
为指数误差取一个更大但更好算的保守误差
\({\Large (1±e)^{n}\le 1±(n+1)e}\)
可算出最终误差为
\({\Large 4e|a+b| + 3e|c|+ 2e|d|}\)
可以看出相加的顺序对误差有影响。较小的数先加,误差更小。
\({\Large (1±e)^{n}\le 1±(n+1)e}\)
这个近似,仍不满意。
又有人发明出一个上限(见[Accuracy and Stability of Numerical Algorithms]3.1)
\({\Large 1+\theta n}\)
其中\({\Large |\theta n|\le \frac{n}{1-ne}}\)
\(n\)越大,误差累积越大。
最后取
\({\Large Gn=\frac{ne}{1-ne}}\)
之前的四数相加就变成
\({\Large \begin{aligned} & (((a ⊕ b) ⊕ c) ⊕ d) \\ & ⊂(a+b)(1±G_3) + c(1±G_2) + d(1±G_1) \\ & ⊂ a + b + c + d ± (a+b)G_3 ± cG_2 ± dG_1 \end{aligned}}\)
pbrt里的\(gamma(n)\)函数就是算\(\frac{ne}{1-ne}\)。
对于乘法rounding
\({\Large \begin{aligned} & a(1±G_i) ⊗ b(1±G_j) \\ & ⊂ ab(1±G_{i+j+1}) \end{aligned}}\)
而\((1 \pm G_i)(1 \pm G_j) = (1 \pm G_{i+j})\)
矩阵变换的误差#
对Vector3进行tansform
\(\begin{bmatrix} m00& m01& m02& m03\\ m10& m11& m12& m13\\ m20& m21& m22& m23\\ m30& m31& m32& m44 \end{bmatrix} \times \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} newX\\ newY\\ newZ\\ 1 \end{bmatrix}\)
\(\begin{aligned} newX & = ((m00 ⊗ x) ⊕ (m01 ⊗ y)) ⊕ ((m02 ⊗ z) ⊕ m03) \\ & ⊂ (m00x(1±G1) ⊕ m01y(1±G1)) ⊕ (m02z(1±G1) ⊕ m03) \\ & ⊂ (m00x(1±G1) + m01y(1±G1))(1±G1) ⊕ (m02z(1±G1) + m03)(1±G1) \\ & ⊂ (m00x(1±G2) + m01y(1±G2)) ⊕ (m02z(1±G2) + m03(1±G1)) \\ & ⊂ (m00x(1±G2) + m01y(1±G2) + m02z(1±G2) + m03(1±G1))(1±G1) \\ & ⊂ m00x(1±G3) + m01y(1±G3) + m02z(1±G3) + m03(1±G2) \end{aligned}\)
可以把最后一项的G2提升为G3。把误差范围提高,不影响正确性。最后得到
\(⊂ (m00x + m01y + m02z + m03) ± G3(|m00x| + |m01y| + |m02z| + |m03|)\)
所以\(newX\)的绝对误差范围是
\(±G3(|m00x| + |m01y| + |m02z| + |m03|)\)
同理可得\(newY\)和\(newZ\)的误差。
3.9.2 保守的ray-bounds相交#
计算光与bounds的相交,允许假相交,但绝对不能漏掉一个。
\({\large t=(X_{1}-O_{x})\frac{1}{D_{x}}}\)
3.9.3 可容错的三角形相交#
3.9.4 交点的误差限制#
见图3.43。如果有一个计算出来的交点,以及误差上限,那么可以保证实际的交点一定在box里。
计算相交可能产生较大的误差。
例如算出某个交点,得到\(t\)值,带误差\(\delta\)。
再生成光
\(P=O+tD\)
对于x轴有
\(x=O_x⊕(t±δ)⊗Dx\)
最后可到误差上限为
\(\gamma_1|O_x| + \delta_t(1 \pm \gamma_2)|D_x|+ \gamma_2|tD_x|\)
可以看出
1.这个误差不受控,我们计算出的t的误差是可控的。但\(O_x\),\(D_x\)可以是任意值,可能非常大。
2.对于\(t\)来说,通常计算相交要进行十次级别的运算,也就是能达到\(1±G10\)级别,也是很大的误差。
所以计算相交可能产生较大的误差。
需要想办法把误差控制在几个ulp之间。
有一种方法是先算一个交点a,再从交点a生成光计算第二个交点。
这样t一定非常小,趋近于0。所以3.13的误差值也会变小。
另一种方法是把交点直接投到面上。
这样不用很多计算。误差也很小。
对于不同shape,有不同的计算方法。
例如球形,球的半径r是已知的,正确的。
而算出来的点到球心的距离可能大于r或小于r,那么就把算出来的xyz以实际的球的r值,做缩放,以匹配r。
\({\Large xNew =\frac{xr}{\sqrt{ x^2 + y^2 + z^2}}}\)
\({\Large xNew = \frac{x⊗r}{\sqrt{x⊗x ⊕ y⊗y ⊕ z⊗z}}}\)
xyz本身带误差。所以有
\({\Large \begin{align} \LARGE & \subset \frac{x(1±e)⊗r}{\sqrt{x(1±e) ⊗ x(1±e) ⊕ y(1±e) ⊗ y(1±e) ⊕ z(1±e) ⊗ z(1±e)}} \\ & \subset \frac{xr(1±e)^2}{\sqrt{x^2(1±e)^2 ⊕ y^2(1±e)^2 ⊕ z^2(1±e)^2}} \\ & \subset \frac{xr(1±e)^2}{\sqrt{(x^2(1±e^2) + y^2(1±e)^2)(1±e) ⊕ z^2(1±e)^2}} \\ & \subset \frac{xr(1±e)^2}{\sqrt{(x^2(1±e)^3 + y^2(1±e)^3) ⊕ z^2(1±e)^2}} \\ & \subset \frac{xr(1±e)^2}{\sqrt{x^2(1±e)^4 + y^2(1±e)^4 + z^2(1±e)^3}} \\ \end{align}}\)
\(z^2\)的\(G3\)提升为\(G4\)。有
\({\Large \subset \frac{xr(1±e)^2}{ \sqrt{ x^2 + y^2 + z^2} \sqrt{(1±e)^4} }}\)
除法也带误差。有
\({\Large \begin{align} & \subset \frac{xr(1±e)^2 } { \sqrt{ x^2 + y^2 + z^2} \sqrt{(1±e)^4}(1±e)} \\ & \subset \frac{xr(1±e)^2 } { \sqrt{ x^2 + y^2 + z^2} (1±e)^3} \\ & \subset \frac{xr(1±G5) }{ \sqrt{ x^2 + y^2 + z^2}} \end{align}}\)
最终需要带上\(1±G5\)的误差。
3.9.5 可容错的光的生成#
例如要生成一个反射光线
先算出交点a,它的误差上下限可以限定出一个长方体,xyz都取大和最小作为对角。
准确的点就在这个长方体里。面是准确的,所以面一定与这个长方体相交。
如果不做处理,直接从a生成光,那么由于误差,a可能会再次与面相交。
现在的方法是先把a沿面的normal方向向外延伸,挪出可能的误差范围,让它不可能再与面相交。
再正常计算。
沿面的normal方向向外延伸的好处,挪动距离最少。而且阴影和反射的效果更好。
见OffsetRayOrigin函数
SpawnRay相关问题
加上错误处理后效果非常明显
处理之前图像有很多黑点noise,就是因为误差导致二次相交。处理完后一眼看去没有noise了。
思考
IEEE保证程序算出来的值与准确值的误差在e之内。
科学家给出一些e基础上的实用的保守近似。
我们拿来跟踪这些误差,算出累积。
在各个层面根据误差做出调整,规避问题。
4 加速#
4.3 BVH#
树形结构。从一个包含了所有物体的bbox为root开始。
大致按质点的3d坐标划分所有物体。
每个节点对应一个bbox,包住所属的物体。
一般把一个节点划分为两个子节点,也就是划分为两组物体。
子节点bbox一定在父节点bbox之内。所以整个子树也都在父节点bbox之内。
物体最终只会存在叶子节点。
一个叶子可能包含多个物体。例如质点非常近甚至重合的物体。
不同节点的bbox可能相交。因为划分是按质点,无关物体实际大小。可能物体超大,就会出现相交。
划分没有一个明确的最优解,一般是用概率等数学手段来得到较好的划分。 你想怎么划分都可以,只要你保证bbox那些数据计算正确,查询起来结果就正确,只是效率有差距。 不过即使是较为简单的划分也比暴力遍历强得多。
http://www-sop.inria.fr/members/Stefan.Popov/media/BVHPacketsOnGPU_IRT07.pdf
https://people.csail.mit.edu/amy/papers/box-jgt.pdf
https://jcgt.org/published/0007/03/04/paper-lowres.pdf
[Realtime Ray Tracing on GPU with BVH-based Packet Traversal][On fast Construction of SAH-based Bounding Volume Hierarchies][An Efficient and Robust Ray–Box Intersection Algorithm]论文顺序#
[Ray Tracing Deformable Scenes Using Dynamic Bounding Volume Hierarchies][Experiences with Streaming Construction of SAH KD-Trees][Realtime Ray Tracing on GPU with BVH-based Packet Traversal][On fast Construction of SAH-based Bounding Volume Hierarchies]pbrt默认就是用的binning方法。依据上面两个论文。
[An Efficient and Robust Ray–Box Intersection Algorithm]论文研究#
[Ray Tracing Deformable Scenes Using Dynamic Bounding Volume Hierarchies]
bvh可以采用任何数量的分叉。这里采用二叉。轴对齐的AABB。
top-down顺序创建bvh#
科学家总结出一种光线与S求交的耗时表达
\({\Large T=2T_{AABB}+ \frac{A(S_{1})}{A(S)}N(S_{1})T_{tri}+ \frac{A(S_{2})}{A(S)}N(S_{2})T_{tri}}\)
\({\Large =2T_{AABB}+\frac{T_{tri}}{A(S)} (A(S_{1})N(S_{1})+ A(S_{2})N(S_{2}))}\)
每次分组的目的,就是要让T尽可能小。
把\(S\)分为两组,有\(2^{N}\)种方法。
找到最佳的划分不现实,我们转而找一个较好的划分。
## 划分S的大致伪代码。有些边界细节可能有误,暂时忽略。
## S为三角形合集,以每个三角形包围盒的质点代表三角形进行计算。
def partition(S):
bestCost = max ## 最优开销
bestAxis = None ## 最优的轴
bestIndex = -1
for axis in [x, y, z]: ## 分别对xyz轴
sort(S, axis) ## 按当前轴排序
## S[i]为[三角形i/点i]的信息
## 设S[i].leftArea为i左边(不包含i)的总包围盒面积。
## 设S[i].rightArea为i右边(不包含i)的总包围盒面积。
S1 = []
S2 = S
## 遍历第一遍。算所有的leftArea
for i = 0 to |S|:
S[i].leftArea = Area(S1) ## 空集面积为无穷大
S1.append(S[i]) ## 添加当前点到S1
S1 = S
S2 = []
## 遍历第二遍。算右边面积。同时评估sah。
for i = |S| - 1 to 0:
S[i].rightArea = Area(S2)
## 算SAH。只需A(S1),N(S1),A(S2),N(S2)四个值就可以进行对比。
sah = SAH(S[i].leftArea, |S1|, S[i].rightArea, |S2|)
if bestCost > sah: ## 如果得到更小的sah。记录下来。
bestCost = sah
bestAxis = axis
bestIndex = i
d把点i从S1挪到S2
## 到此已经得到了最好的划分
对于划分平面的挑选,作者尝试了平均分、用包围盒的面分、以质点分。得到的结果相近。
求交#
如果只判断光与bvh是否相交。就很简单。
bool intersect(node, ray):
if node is leaf:
return node.triangle.intersect(ray)
if intersect(node.left, ray) or intersect(node.right, ray):
return True
return False
如果要获得最近的相交,就不好搞。
pbrt貌似有优化,有点绕,一下子没看懂它怎么得到最近的,先不管。
三角形发生变化时的bvh更新流程#
创建的bvh的时间点#
论文研究#
[Realtime Ray Tracing on GPU with BVH-based Packet Traversal]这个论文貌似没具体讲质点如何映射到bin??只能去看它参考的论文。
论文研究#
[On fast Construction of SAH-based Bounding Volume Hierarchies]- 每个bin包含的数据?count和bbox
- bin的数量?设定bin数量为\(K\),可按需设置,4和16都是可行的。pbrt定为12。
- 选轴每次划分先遍历所有三角形算出整个bbox。根据整个bbox,选出跨度最大的轴,只在这个轴上划分。
- 如何生成bin信息?遍历三角形集合。算出每个质点在选定轴上的最大跨度中,所处的位置。根据这个位置确定bin的index。比如处于跨度1/4处,有12个bin,那么就选1/4处也就是第3个bin。确定index后,对应bin的count+=1。并且把当前三角形的bbox和对应bin的bbox进行融合,如果bin的bbox包不住三角形bbox,就要扩大bin的bbox以包住三角形。所以最后每个bin的数据是质点落在对应范围内的三角形的总数和总的bbox。
如何评估sah?
## 大致伪代码 final_cost = max for i = 0 to |bin|: ## 遍历所有bin count_L = 0 count_R = 0 bbox_L bbox_R ## 算左边的count和总的bbox for j = 0 to i: count_L += bin[j].count bbox_L += bin[j].bbox ## 算右边的count和总的bbox for j = i to |bin|: count_R += bin[j].count bbox_R += bin[j].bbox cost = (count_L * bbox_L.area() + count_R * bbox_R.area()) / 总bbox面积 if final_cost > cost: ## 得到了更好的cost final_cost = cost ## 到此得到了最好的cost
4.3.1 BVH的创建#
见上述论文
4.3.2 SAH#
见上述论文
4.3.3 HLBVH#
hierarchical linear bounding volume hierarchy
4.4 kd-tree#
[Photorealistic Rendering using the PhotonMap]创建:
对一堆三维空间点进行划分,实现logN复杂度查询某个点最临近的k个点。
把所有点按一排数组看待,不断从中间分成两段,作为左右子树。
每层按某个坐标轴划分,xyz依次来。
左边的子树的坐标都小于等于当前节点,右边都大于等于当前节点。
每次找位于正中间的点,用快速选择算法,见上面链接和算法导论。
找中间的点,确保了树的平衡。也确定了每个节点的index。 子树index也很好算,左边就是
i*2+1,右边就是i*2+2。 所有节点可存在一个数组里。
knn查询:
维护一个类似priority_queue的数据,存候选点和距离,最多存k个候选。 能快速删除其中的最大距离。
维护候选数据中的最大距离。
从index0根节点开始。如果候选未满,插入当前节点。更新候选数据。
正常情况下递归搜索左右子树。
如果此时候选已满,可能有机会剪枝。 比如此时按x轴分成左右。 如果目标点在当前节点的左边,目标点与当前点在x上的距离为A。 那么根据划分的性质,当前点的右子树中所有的点与目标点的三维距离一定大于A。 如果此时候选已满,且候选最大距离比A要小,那么右子树就没必要再查了。
5 色彩和辐射度量学#
5.2#
5.2.1 XYZ色彩#
5.2.2 RGB色彩#
5.3 RGBSpectrum#
5.4 Radiometry 辐射度量学#
几何光学已经足够建立起pbr的光模型。
光的衍射和干扰很难实现
5.4.1 基本的物理量#
energy Q#
一个光子所带的能量
flux/Radiant flux#
\({\Large \Phi=\frac{dQ}{dt}}\)
功率按时间积分得到能量
Irradiance / Radiant exitance#
辐照度/辐射出射度
单位面积上的辐射功率。一个是入,一个是出。
\({\Large E = \frac{d\Phi}{dA}}\)
A是趋近于0的,所以相当于一点上的辐射功率。
点光源
\({\Large E = \frac{\Phi}{4πr^2}}\)
这里可以看出能量按距离的平方衰减。
按面积积分得到辐射功率。
solid angle / intensity#
辐射强度intensity,为单位球面度的辐射功率,和Irradiance类似。
\({\Large I=\frac{d\Phi}{dω}}\)
intensity按立体角积分得到Φ
Radiance#
最后最重要的辐射率
Irradiance给出的是单位面积(一点)上的辐射功率,但是没有区分方向。
\({\Large L=\frac{dE}{dω}}\)
\({\Large L=\frac{d^2\Phi}{dAdω}}\) (这里书上写错了,漏掉了2次)
5.4.2 入射/出射辐射率函数#
\({\Large L_i(p, ω)}\)
5.4.3 Photometry 光度学#
https://en.wikipedia.org/wiki/Photometry_(optics)
所有辐射度量学的物理量都可以转化成对应的光度学物理量。通过对spectral response curve积分。
5.5 辐射度量学的积分#
渲染中最常见的操作是对辐射度量学物理量进行积分。
\({\Large L=\frac{dE}{dω}}\)
\(L_i(p, ω)\)描述了点p上不同ω上的光能。
积分考虑的是所有光。写成积分的形式更优雅统一。并且后续可以用蒙特卡洛方法处理。
https://zhuanlan.zhihu.com/p/33464301
后面brdf也是用这种积分形式,得统一理解。
5.5.1 对立体角积分#
5.5.2 球坐标积分#
\({\LARGE \frac{y}{2πr} = \frac{dθ}{2π}}\)
横向微小长度x。θ处的横切面半径为\({\Large rsinθ}\),有
\({\LARGE \frac{x}{2πrsinθ} = \frac{dφ}{2π}}\)
得
\({\Large x=rdφsinθ}\)
针对单位球体,r=1
\({\Large dw= dA = xy=r^2sin\theta d\theta d\phi = sin\theta d\theta d\phi}\)
最终的半球积分形式就是\({\Large sinθdφdθ}\),\(\theta\)从0到\(\pi/2\)积90度,\(\phi\)从0到\(2\pi\)积一圈。
\({\Large E(p, n) = \int_{0}^{2\pi } \int_{0}^{\frac{\pi}{2} } Li(p, θ, φ) cosθ sinθ dθ dφ}\)
5.5.3 转化为对面积积分#
对立体角积分还可以转化为对面积积分。可用于简化计算。
例如对于方程
\({\Large E(p, n) = ∫Li(p, w)|cosθ|dw}\)
是针对一定范围的立体角积分。
如果要针对一个四边形求E。那么用立体角就不好算。
见图5.17
首先按比例算
\({\Large dw/4π = dA/4πr^2}\)
\({\Large dw = \frac{dA}{r^2}}\)
一般情况dA不是正对着点p,要加上\(cosθ_o\)。
\({\Large dw = \frac{cos\theta_o dA}{r^2}}\)
替换后方程变为
\({\Large E(p, n) = ∫_{A}L |cos\theta_i| \frac{cos\theta_o dA}{r^2}}\)
5.6 表面反射#
透明物质比较复杂,要考虑光在物质内部(表面以下)传播,入射点和出射点可能有一定距离。
bssrdf brdf的一般形式。 可更精确地描述透明物质。
5.6.1 BRDF (bidirectional reflectance distribution function)#
先有入射光\(Li(p, ωi)\)。想要得到某个出射方向ωo的光\(Lo(p, ωo)\)。
这里的积分又跟之前一样,考虑的是所有方向上的所有光对ωo的贡献。
第八章详细讲brdf。
\({\Large \int_{H^2(n)}f_r(p, \omega_o, \omega')cos\theta'd\omega' \le1}\)
其中\(\theta'\)是跟随每一个\(\omega'\)的。
最后形成了重要的方程
\({\Large L_o(p, \omega_o)= \int_{S^2}f(p, \omega_o, \omega_i)L_i(p, \omega_i)|cos\theta_i|d\omega_i }\)
半球范围内所有的入射光对\(\omega_o\)方向的光能,经过brdf处理,再积起来,就得到了p点向\(\omega_o\)方向的光能。
5.6.2 bssrdf#
6 camera#
6.2 相机投影#
相机空间的坐标如何投影到最终的2d屏幕
- screen spacez值在0-1之间
- ndc space见图6.1在xy平面从(0, 0)到(1, 1),在z方向的范围是(0, 1)。
ndc这个东西也是各家可以自己定的。有的xyz是从0到1,有的xyz是从-1到1。
我先以-1到1来计算
对于不同的ndc和相机坐标的左右手,结果矩阵是不一样的。
6.2.1 正交#
较为直接的mapping。没有近大远小的立体效果。
正交的输入,基本就是定义一个立方体。立方体之外的点都丢掉。
保留距离和角度关系。平行的线显示出来还是平行。
坐标在各个轴计算之于立方体范围的比例,然后把比例乘到ndc即可。
相机坐标系下。给定左右边界lr,上下边界tb,near平面n,far平面f。
\({\Large \frac{X-l}{r-l}=\frac{newX+1}{2}}\)
就是按比列投到-1和1区间
算得
\({\Large newX=2x/(r-l) - (r+l)/(r-l)}\)
同理
\({\Large newY=2y/(t-b) - (t+b)/(t-b)}\)
\({\Large newZ=2z/(f-n) - (f+n)/(f-n)}\)
那么可以凑出变换矩阵
\(\begin{bmatrix} 2/(r-l) & 0& 0& -(r+l)/(r-l)\\ 0& 2/(t-b)& 0& -(t+b)/(t-b)\\ 0& 0& 2/(f-n) & -(f+b)/(f-n)\\ 0& 0& 0& 1 \end{bmatrix}\)
这个矩阵乘 \(\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}\)能得到\(\begin{bmatrix} newX\\ newY\\ newZ\\ 1 \end{bmatrix}\)
\(r+l=0\)\(r-l=2r\) (即立方体宽)w\(t+b=0\)\(t-b=2t\) (即立方体高)h
最终的正交矩阵
\(\begin{bmatrix} 2/w& 0& 0& 0\\ 0& 2/h& 0& 0\\ 0& 0& 2/(f-n)& -(f+b)/(f-n)\\ 0& 0& 0& 1 \end{bmatrix}\)
6.2.2 透视/立体#
近大远小。不保留距离和角度关系。平行线也不再平行显示。
从上方视角来看,根据相似三角形关系。
\(Xp/X = n/Z\)\(Xp = Xn/Z\)
同理侧面来看
\(Yp/Y = n/Z\)\(Yp = Yn/Z\)
然后算Xp和Yp在near平面的比例关系。Xp和Yp代入之前的newX,newY。
\(newX=2x/(r-l) - (r+l)/(r-l)\)\(\ \ \ \ \ \ \ \ \ \ \ \ \ \=2Xn/Z(r-l) - (r+l)/(r-l)\)
\(newY=2Yn/Z(t-b) - (t+b)/(t-b)\)
\(newZ\)的情况。一开始有点难理解。查了一圈有好几种说法。
如果按简单的线性映射,再凑矩阵。
\((Z-n)/(f-n) = (newZ+1)/2\)\(newZ=2Z/(f-n) - (f+n)/(f-n)\)
发现很难像正交那样凑出来。
\(xy\)正常凑。填上AB,再从结果反解AB。
\(\begin{bmatrix} 2n/(r-l) & 0& -(r+l)/(r-l)& 0\\ 0& 2n/(t-b)& -(t+b)/(t-b)& 0\\ 0& 0& A& B\\ 0& 0& 1& 1 \end{bmatrix}\)
注意\(newX\)和\(newY\)都和Z相关,是1/Z的关系。
如果用\([X, Y, Z, 1]\)去乘,得到的结果需要/Z才是最终映射值。
换句话说得到的结果是最终映射值乘Z。
所以映射方程是\(AZ+B=(newZ)Z\)。这样映射,顺序是不会打乱的,所以正确性没问题。
对于x和y也是一样的。
就是统一构造了一个Z。
A下面的1也是这个原因,为了构造Z。
这样用\([X, Y, Z, 1]\)乘出来就是\([ZnewX, ZnewY, ZnewZ, Z]\)。最后统一除以Z,就得到了最终的(-1,1)的映射。
对于\(AZ+B=(newZ)Z\)
已知n映射到-1,f映射到1。
填上nf两个已知的映射。就能解出AB了。
\(An+B=(-1)n\)\(Af+B=(1)f\)
解得
\(A = (f+n)/(f-n)\)\(B = 2fn/(n-f)\)
得到Perspective矩阵
\(\begin{bmatrix} 2n/(r-l)& 0& -(r+l)/(r-l)& 0 \\ 0& 2n/(t-b)& -(t+b)/(t-b)& 0\\ 0& 0& (f+n)/(f-n)& 2fn/(n-f)\\ 0& 0& 1& 1 \end{bmatrix}\)
再有
\(r+l=0\)\(r-l=2r\) (即n平面宽)w\(t+b=0\)\(t-b=2t\) (即n平面高)h
得
\(\begin{bmatrix} 2n/w& 0& 0& 0 \\ 0& 2n/h& 0& 0\\ 0& 0& (f+n)/(f-n)& 2fn/(n-f)\\ 0& 0& 1& 1 \end{bmatrix}\)
高和宽与fov/aspect ratio相关。fov可分水平和垂直,我们用水平fov。
\(tan(fov/2) = w / 2n\)\(w = 2ntan(fov/2)\)\(h = w / asp\)
得到用fov和asp表示的矩阵
\(\begin{bmatrix} 1/tan(fov/2)& 0& 0& 0 \\ 0& asp/tan(fov/2) & 0& 0\\ 0& 0& (f+n)/(f-n)& 2fn/(n-f)\\ 0& 0& 1& 1 \end{bmatrix}\)
另一种角度
http://learnwebgl.brown37.net/08_projections/projections_perspective.html
这里他是从误差的角度去看,直接引入非线性映射。
越近的点变化幅度越大,所以误差越小。同理越远的点允许误差越大。
7 采样和重建#
采样理论。从连续函数上采集样本,再用这些样本重建相似的函数。
Sampler的实现
Filter类决定如何blend像素附近的像素,并确定最后的像素。
Film类将样本进行累积,计算像素。
7.1 采样理论#
可以对每个像素进行一次精确的采样,直接作为最终输出。
7.1.1 频域和傅立叶变换#
转换出来的信息就是原函数的频域分布。
频域可以从另一个角度看函数的性质。
傅立叶逆变换
Dirac delta distribution
7.1.2 理想化采样和重建#
首先有\(\delta\)函数
https://mathworld.wolfram.com/DeltaFunction.html
https://en.wikipedia.org/wiki/Dirac_delta_function
\(\delta(x) = \left\{\begin{matrix} +\infty, &x=0 \\ 0, &x \ne 0 \end{matrix}\right.\)
\(\int_{-\infty}^{\infty }\delta (x)dx=1\)
它不是一个普通意义的函数。实际上是一种分布。在0处一柱擎天。
shah函数/Dirac comb
\({\Large Ш_{T}^{}(x)=\sum_{i=-\infty}^{\infty} \delta (x-iT)}\)
https://mathworld.wolfram.com/ShahFunction.html
https://en.wikipedia.org/wiki/Dirac_comb
把\(\delta\)函数这样处理就变成一个周期性的分布。就像一个梳子,所以用Ш这个符号。
\(i\)为所有整数。
\(T\)为周期,也作为采样率。
如果再乘上一个\(f(x)\),变成
\({\Large Ш_{T}^{}(x) f(x)=\sum_{i=-\infty}^{\infty} \delta (x-iT) f(iT)}\)
一般会取unit impulse即\(\delta(0) = 1\),刚好就是是对\(f(x)\)进行采样。见图7.4。
选一个重建过滤函数\(r(x)\),进行卷积操作,可以用这些采样点生成结果函数\(\tilde f\)。
\((Ш_T(x)f(x))\otimes r(x)\)
convolution 卷积#
有\(f(x)\)和\(g(x)\)。
把\(g(x)\)按y轴翻转,即变成\(g(-x)\)。
得到两个确定的函数/图形。
这时给\(g(-x)\)一个变量\(t\)作为x轴上的位移。有\(g(t-x)\)。
那么随着\(t\)的改变,\(g(-x)\)就能在x方向滑动。
对于某一个\(t\),可计算\(f(x)g(t-x)\),得到一个变量为\(x\)的函数。把这个函数对所有\(x\)积分,就得到了\(t\)对应的卷积值。
对于每个\(t\),都有一个卷积值,那么就形成了一个函数\(Juan(t)\)。
就得到了卷积\(Juan(t)=f(x)\otimes g(x)\)
写成积分形式
\({\Large Juan (t)=\int_{-\infty}^{\infty}f(x)g(t-x)dx =f\ast g}\)
Nyquist frequency
https://www.shadertoy.com/view/XlcSz2
https://www.shadertoy.com/view/MdjGR1
接下来就是一些图像/信号处理的知识,涉及傅立叶变换、各种滤波等等。可以大胆地说出,看不懂。
至少学一些基本知识,有个大致概念。其他有缘再见。
可以直接转10.4.3看代码。看看怎么对图像进行resampling,然后生成mipmap。
7.1.3 锯齿#
7.2 采样接口#
7.3 分层采样#
7.8 图形重建#
7.8.1 滤波函数#
https://en.wikipedia.org/wiki/Sinc_function
https://en.wikipedia.org/wiki/Lanczos_resampling
sinc滤波是一种理想的滤波,可以去除某个给定频率之上的部分,且不影响低频部分。
\(sinc(x) = \frac{sin(x)}{x}\)
实数域上的积分为\(\pi\)
进行normalize后
\(sinc(x) = \frac{sin(\pi x)}{\pi x}\)
实数域上的积分为1
\(sinc(0)=1\)
lanczos重采样#
lanczos是一种低通滤波,同时可用于样本之间的平滑插值。
代码实现:
\(L(x)=\left\{\begin{matrix} \frac{sinc(\pi xa)}{\pi xa} \frac{sinc(\pi x)}{\pi x} & x \le 1\\ 0& x>1 \end{matrix}\right.\)
\(a\)取2。
Gamma Correction#
8 反射模型#
brdf/btdf统称bsdf
- 对于现象的建模根据现象/感觉建模。比如常见的roughness。
- 模拟基于物理/几何等的模拟
- 光波等原理。物理光学较为深层次的模拟。更耗资源,且通常并没有得到更好的效果。
几何光学
基本术语
主要分4类
- diffuse光向所有方向发散如果是均匀的话是完美diffuse,实际不常见。
- glossy specular光向一个较小的范围发散。高光。比如塑料。可显示模糊的倒影。
- perfect specular光向一个极小的范围发散。 完美镜面反射。镜子
- retro reflection原路返回
各向异性的例子。衣物,cd表面,brushed metal。
几何设置#
\(cos(θ) = dot(w, n) = w.z\)
针对W可做一系列helper函数。求一些常用值。
\(x = r sin(θ) cos(φ)\)\(y = r sin(θ) sin(φ)\)\(z = r cos(θ)\)
现在要算u变化时,xyz对应的变化率。也就是分别对xyz求u的偏导数,dp/du。
dx/du
= d (r sin(θ) cos(φ)) / du
= rsin(θ) d cos(u*phiMax)/du // float u = phi / phiMax;代入
= -rsin(θ)sin(φ)phiMax
= -y * phiMax
dy/du
= d(r sin(θ) sin(φ)) / du
= rsin(θ) d sin(u*phiMax) / du
= rsin(θ)cos(φ)phiMax
= x * phiMax
dz/du
= d (r cos(θ)) / du
= 0
Vector3f dpdu(-phiMax * hitPoint.y, phiMax * hitPoint.x, 0);
同样可算出dp/dv
Vector3f dpdv = Vector3f(hitPoint.z * cosPhi, hitPoint.z * sinPhi, -radius * std::sin(theta))
* (thetaMax - thetaMin);
interaction的n和shading.n都初始化为Cross(dpdu, dpdv)。
BSDF的初始化中
其实就是dpdu和dpdv和他们的Cross
- n指向外部。…
本地坐标
brdf/btdf的实现不应关心Wi和Wo是否在同一半球。
8.1 基本接口#
f函数。也就是brdf。
8.1.1 反射率#
hemispherical-directional reflectance半球-方向反射率
\({\Large \rho_{hd}(w_o)=\int_{H^2(n)} f_r(p, w_o, w_i)|cos\theta_i|dw_i }\)
一束入射光\(w_o\)对半球范围所有方向(\(w_i\))的贡献(\(f_r(p, w_o, w_i)\)),加起来。
一般都是用蒙特卡洛算积分。
不带方向的反射率为ρhh
d
8.1.2 BxDF SCALING ADAPTER#
8.2 SPECULAR REFLECTION AND TRANSMISSION#
镜面的反射和传输相对简单。
\(θ_i=θ_o\)\(φ_i=φ_o+π\)
传输就是折射
\({\Large \eta_isin\theta_i = \eta_t sin\theta_t}\)
8.2.1 FRESNEL#
例如落地玻璃,正对着看,主要为折射。而越平着看,越体现为反光。
折射率又和物质的导电性质有关
给定两种材质的折射率,入射角,fresnel方程可算出反射和折射的比例。
fresnel方程的原理需要光学,电磁学相关。咱忽略。
Schlick给出了一种近似算法。
8.2.2 specular reflection#
8.2.3 specular transmission#
镜面的btdf
8.3 LAMBERTIAN REFLECTION#
8.4 MICROFACET MODELS 微小面模型#
点被山峰遮挡
点在阴影里
光在山谷里多次反射。
8.4.1 Oren–Nayar 漫反射#
V型微小面按高斯球形分布。参数σ,表示粗糙程度,微小面倾角的标准差。
对于V型微小面这种模型,多次反射的问题只需在相邻V型之间考虑。
给定σ,θi和θo就可以算出反射率了。
8.4.2 微小面分布函数#
基于微小面的模型,对于金属/塑料/毛玻璃等材质的镜面反射和传播有较好的表现。
微分面的分布函数D(ωh)。类似一个概率密度。
分布函数必须normalize,才能保证物理上正确。
图8.15。分布函数必须满足条件。给定dA,函数生成的投影面积也必须为dA。
积分形式
\({\LARGE \int_{H^2(n)}D(\omega_h)cos\theta_hd\omega_h=1}\)
BeckmannDistributionTrowbridgeReitzDistribution,即GGX。 GGX更符合实际物体的物理特性。
代码流程#
Sample_f采样方向,走微小面的Sample_f。Sample_wh()根据\({\Large \omega_{o}}\)随机采样出一个normal\({\Large \omega_{h}}\)。微小面采样见14.1.1
8.4.3 MASKING AND SHADOWING#
规则的积分形式
\({\LARGE cos\theta=\int_{H^2(n)}G_1(\omega,\omega_h)max(0,\omega \cdot \omega_h)D(\omega_h)d\omega_h}\)
这里有一层含义,G函数是之于D函数基础上的。是要配合的,不是独立的。
\({\LARGE G_1(\omega)=\frac{A^+(\omega)-A^-(\omega)}{ A^+(\omega)}}\)
和\(G_1(\omega,\omega_h)\)的区别是此时\(\omega_h\)隐含在了面积里。
有关系\({\LARGE G_1(\omega)=\frac{1}{1+\Lambda(\omega)}}\)
`A Reflectance Graphics Model for Computer <https://graphics.pixar.com/library/ReflectanceModel/paper.pdf>`__#
这个论文是82年的Cook-Torrance模型。
论文研究 `Microfacet Models for Refraction through Rough Surfaces <https://www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf>`__#
这个论文主要讲折射的微表面模型,引入了GGX。
宏观表面的BSDF记作\({\Large f_s(i, o, n)}\),描述入射i,出射o,normal n条件下得到的能量比例。
如果细分成反射和折射,那么就是BRDF(\(f_r\))和BTDF(\(f_t\))。
\(f_s\)是\(f_r\)和\(f_t\)的和。
可以不纠结每个微小表面,而是整体来看,用统计的方法(\(D_m\))来描述所有微表面的normal的分布。
之前学习过,发明出来的\(D_m\)必须保证物理上的正确性。
- \({\Large 0 \le D(m)}\)任意m的D值大于等于0
- \({\Large 1 \le \int D(m)d\omega_m}\)\(\omega_m\)为某个m对应的立体角。即所有方向的D(m)加起来大于等于1。
- \({\Large (v \cdot n) = \int D(m)(v\cdot m)d\omega_m}\)给定任意方向v,考虑v在normal上的分量。左边的宏观值与右边的微观分量和要相等。这是一个通用的式子,对任意v有效。很多资料给出的是\({\Large \int D(m)(m \cdot n)d\omega_m =1}\)这其实是\({\Large v=n}\)的特殊情况。
Shadowing-Masking函数\({\Large G(i, o, m)}\)描述normal为m的微小表面,入射i,出射o情况下能被看到的概率。
- \({\Large 0 \le G(i, o, m) \le 1}\)是一个普通的概率值
- \({\Large G(i, o, m) = G(o, i, m)}\)来去对称
- 如果\({\Large (i \cdot m) \le 0}\)或\({\Large (o \cdot m) \le 0}\),\({\Large G(i, o, m) = 0}\)看微表面的背面,G一定为0。论文里带上了\({\Large (i \cdot n)}\)和\({\Large (o \cdot n)}\),意思是扩展为正反面都成立。更严谨。
论文研究#
`Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs <https://www.jcgt.org/published/0003/02/03/paper.pdf>`__
。。。
9 material#
引入BSDF类。包含一系列bxdf。
9.1 BSDF#
brdf和btdf的集合。
BSDF实例在SurfaceInteraction里
9.2 material#
10 texture#
10.1 采样和抗锯齿#
为了在texture函数中实现抗锯齿,需要解决两个问题。
- 必须计算texture空间中的采样率。屏幕空间的采样率是已知的,根据图像大小和像素的采样率。但必须确定场景中某个面上的采样率。
- 得到texture采样率以后,必须依据采样原理来计算texture值,使其不高于采样率能承载的最大频率波动。(除去超出奈奎斯特极限的频率)
10.1.1 找出texture的采样率#
预先总结,这一节实际讲如何计算屏幕空间的xy坐标与texture的uv坐标的相对变化。
[THOMAS' CALCULUS]13章偏微分。\({\Large f(x, y) ≈ f(x_0, y_0) + (x - x_0)\frac{∂f}{∂x}(x_0, y_0) + (y - y_0)\frac{∂f}{∂y}(x_0, y_0)}\)
算出初始点(x0, y0)的值和对应的偏微分,就可以估算其他点(x, y)的值。
从屏幕坐标(x,y)映射到texture(可看成一张图)的(u,v)
\({\Large (x-p_x, y-p_y, z-p_z) \cdot n = 0}\)
\({\Large xn_x + yn_y+zn_z -n\cdot p = 0}\)
这样得到了切面方程。
\({\large p=o+t(dir)}\)
的t
有光与面的求交公式
\({\LARGE t=\frac{-n\cdot o - d}{n\cdot dir}}\)
tx和ty有了,px和py也有了。
对于rx有
\({\Large p_x\approx p(x_0, y_0) + (x-x_0)\frac{∂p}{∂x}(x_0, y_0) + (y - y_0)\frac{∂p}{∂y}(x_0, y_0)}\)
对于rx,y的变化为0,那么
\({\Large p_x\approx p(x_0, y_0) + (x-x_0)\frac{∂p}{∂x}(x_0, y_0)}\)
由于辅助光的创建方式,\(x-x_0=1\)。有
\({\Large p_x\approx p(x_0, y_0) + \frac{∂p}{∂x}(x_0, y_0)}\)
\({\Large \frac{∂p}{∂x}(x_0, y_0) \approx p_x - p(x_0, y_0) }\)
dpdx = px - p;
dpdy = py - p;
\({\large p_1(x, y) = newX}\)\({\large p_2(x, y) = newY}\)\({\large p_3(x, y) = newZ}\)
dpdx和dpdy的本质是场景内三维坐标,对于屏幕空间二维坐标的变化率。
dpdu和dpdv在之前的章节有详细的推导。在这里被用上了。这里还是运用近似,这次xy同时移动。
\({\Large p'\approx p(x_0, y_0) + \Delta x\frac{∂p}{∂x} + \Delta y\frac{∂p}{∂y} \approx p(x_0, y_0) + \Delta u\frac{∂p}{∂u} + \Delta v\frac{∂p}{∂v} }\)
解方程
\({\Large p'_x -p_x = \Delta u\frac{∂p_x}{∂u} + \Delta v\frac{∂p_x}{∂v}}\)
\({\Large p'_y -p_y = \Delta u\frac{∂p_y}{∂u} + \Delta v\frac{∂p_y}{∂v}}\)
\({\Large p'_z -p_z = \Delta u\frac{∂p_z}{∂u} + \Delta v\frac{∂p_z}{∂v}}\)
10.1.2 滤波#
可以用box filter进行AA。目前我代码抄过来有问题。
10.2 texture坐标的生成#
常见的各种mapping方法
多数情况没有一个通用的完美的方法来映射texture。比如球体靠近极点的地方一定会有失真。
10.2.1 2d(uv)mapping#
10.3 texture接口#
10.4 image texture#
是最常用的texture
10.4.1 texture存储管理#
10.4.3 mip maps#
mipmapping是最流行的反走样方法。
频率如何理解?#
Nyquist limit/Nyquist frequency#
图10.10两种算法对比。EWA细节上更好。trilinear interpolation在边缘处细节丢失。
resize涉及采样原理。
因为图片尺寸只可能变大,所以不会引入走样。走样的本质起因是想把图片缩小。
详细流程见MIPMap::resampleWeights()
从一个原始图像生成mipmap的流程
如果原始图像长宽不是2的次方。需要放大到下一级2的次方。长宽不一定要相等。
先有重采样weight函数。
MIPMap::resampleWeights(int oldRes, int newRes)
//对于一串数据,从oldRes长度放大到newRes长度。
i从0到newRes循环
center = (i + .5f) * oldRes / newRes; //算出对应原始index
以center为中心取4个index做Lanczos操作
记录每个i的4个index和对应的Lanczos数据,作为weight。weight要做normalize。
对于2d图像。横竖两个方向都要做一次重采样。
对于每一行
i从0到newRes循环
用resampleWeights算出的4个index和weight,结合原始图像的值,算出新值。
此时得到图a
对于每一列
i从0到newRes循环
一样的方法,不过这次是weight结合图a的值,算出最终值。
此时完成了放大图像到2的次方长宽。
最后生成pyramid。下一级图像每4个值一组,就像一个个田字,每个田算平均值,作为一个点,形成了上一级的图像。
这样不断缩小一半。就做好了mipmap。
trilinear interpolation/三线性插值#
11 volumn scattering#
这一章讲光如何被participating media(空间中的大量粒子)影响。
volumn scattering模型的基础:大量的粒子形成一个统计学框架,而不是去死算每一个粒子。
用participating media可以模拟各种烟、云、激光、次表面等。
11.1 VOLUME SCATTERING PROCESSES#
影响radiance分布的3个主要过程
吸收:光能转换成其他能量比如热能。radiance减少。
发光:发光粒子导致radiance增加。
散射:radiance与粒子碰撞改变方向。
11.1.1 吸收#
吸收率写作\(\sigma_a\),是一个概率密度,表示光每传播一单位距离时被吸收的量。
有一些radiance到达点p
\({\Large Li(p, -\omega)}\)
经过一个微小距离\(dt\),出射能量变为
\({\Large Lo(p, \omega)}\)
吸收率的作用体现为
\({\Large Lo(p, \omega) - Li(p, -\omega) }\)
\({\Large = dLo(p, \omega) = -\sigma_a Li(p, -\omega)dt}\)
这是一个微分方程\({\Large y' = -\sigma_ay}\)
\({\Large y = y_0 e^{-\sigma t} }\)
12 光源#
12.1 发光#
Incandescent白炽灯 即 tungsten钨丝灯#
Halogen卤素灯#
Gas-discharge lamps 气体放电灯#
Led#
electroluminescence
12.1.1 黑体辐射源#
12.2.1 检测光是否被阻挡#
12.3 点光源#
12.4 DISTANT LIGHTS/directional light#
其实近似于无限远的点光源
12.5 AREA LIGHTS#
绑定模型,从模型表面发光。
12.6 INFINITE AREA LIGHTS#
13 蒙特卡洛积分#
我们用到的积分方程一般没有解析解。那么就得考虑数值解。
正确使用随机,在算法设计领域是革命性的。
随机算法分两大类
- 拉斯维加斯每次的输出都是一致的比如快速排序。每次选pivot可以是随机的,但是最终结果是精确的,只要输入相同,结果一定相同。
- 蒙特卡洛每次的输出不一致,是随机性的,但是平均结果是基本正确的。可理解为每次的结果基本正确,有时好一点有时坏一点。如果多算几次,取平均值,基本能保证较好的结果。
13.1 概率#
[Introduction to Probability Models][A FIRST COURSE IN PROBABILITY]cumulative distribution function(CDF)\(P(x) = Pr(X\le x)\)
即所有小于等于x的分布的和
probability density function概率密度函数,写作\(p(x)\)。13.1.1 连续随机变量#
渲染领域,连续随机变量比离散随机变量更常见。
容易生成
可先生成标准平均随机变量,再进行变换。
pdf积起来就是cdf
\({\Large P(x \in [a,b]) = \int_{a}^{b}p(x)dx}\)
cdf微分就是pdf
\({\Large p(x)=\frac {dP(x)}{dx}}\)
整个pdf下方的面积一定是1。
13.1.2 期望值和方差#
函数的期望值定义
\({\Large E_p[f(x)] = \int_{D}^{} f(x)p(x)dx}\)
方差
\({\Large V[f(x)] = E[(f(x)-E[f(x)])^2]}\)
13.2 monte carlo estimator#
假设要算这样的积分
\({\Large \int_{a}^{b} f(x)dx }\)
可以做一个所谓蒙特卡洛估算子。
\({\Large F_N=\frac{b-a}{N} \sum_{i=1}^{N}f(X_i)}\)
看看期望值
\({\Large E[F_N] = E[\frac{b-a}{N} \sum_{i=1}^{N}f(X_i)] }\)
\({\Large = \frac{b-a}{N} \sum_{i=1}^{N}E[f(X_i)] }\)
\({\Large = \frac{b-a}{N} \sum_{i=1}^{N} \int_{a}^{b} f(x)p(x)dx }\)
因为Xi是平均分布,所以p(x)=1/(b-a)。
\({\Large = \frac{1}{N} \sum_{i=1}^{N} \int_{a}^{b} f(x)dx }\)
\({\Large = \int_{a}^{b} f(x)dx }\)
可以看到把积分问题转到概率框架下,得到的期望值是积分本身。
对于非均匀分布,可以做这样的估算子。
\({\Large F_N=\frac{1}{N} \sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}}\)
\({\Large E[F_N]=\frac{1}{N} \sum_{i=1}^{N} \int_{a}^{b}\frac{f(x)}{p(x)}p(x)dx}\)
\({\Large = \int_{a}^{b} f(x)dx }\)
同样的结果。这个就是蒙特卡洛积分的理论依据了。采样本,除pdf,做平均,期望值和积分相等。
可以自己手动模拟试试。给一个函数任意造pdf,再模拟多次采样,结果是一样的。
那么怎么选pdf。不同的pdf会造成不同的方差,效果可能非常大。
最简单的是平均采样。
如果pdf和原函数f形状相似,方差就小。见后面的重要性采样相关内容。
13.3 对随机变量采样#
13.3.1 INVERSION方法#
看懂图13.1/13.2/13.3
\({\Large cdf(x)=\int_{0}^{x} pdf(x')dx'}\)。
\({\large cdf(X)=\xi}\)
\({\large X=cdf^{-1}(\xi)}\)
所以叫INVERSION方法。
[Introduction to Probability Models]这本书11.2.1章的内容。其中积分域要注意是从有分布的地方开始到x,不一定是从0开始。
pow(x, n)分布的采样#
一般做成\(pdf(x) = cx^n\)
用c把pdf(x)的积分值限定在1,积分上下限可以按需取值。
算出c。那么pdf(x)就有了。再按上述方法得出cdf反函数。
指数分布采样#
体渲染会用到,对指数函数在0到无穷大上采样。
\({\Large f(x) = ce^{-ax}}\)
\({\Large \int_{0}^{\infty} ce^{-ax}dx =1}\)
\({\Large -\frac{c}{a}e^{-ax}|_{0}^{\infty} =1}\)
\({\Large 0 - (-\frac{c}{a}) =1}\)
\({\Large c = a}\)
所以normalize后的pdf函数为
\({\Large pdf(x) = ae^{-ax}}\)
积分
\({\Large \int_{0}^{x} ae^{-ax'}dx' = -e^{-ax}|_{0}^{x} = 1 - e^{-ax}}\)
求逆
\({\Large y = 1 - e^{-ax}}\)
\({\Large e^{-ax} = 1-y}\)
\({\Large y^{-1} = -\frac{ln(1-x)}{a}}\)
采样
\({\Large X = -\frac{ln(1-\xi)}{a}}\)
Piecewise-Constant 1D#
就是Distribution1D的实现
13.3.2 REJECTION METHOD#
不断地对p(x)采样,得到ξ和X,如果(X, ξcp(X))在f(X)图像下方,就认为对f(x)采样成功,取(X)。
13.5 在不同分布之间变换#
先体验离散的例子
所有X的分布。和为1。
\({\large \begin{matrix} f(0)=0.1 \\ f(1)=0.2 \\ f(2)=0.4 \\ f(3)=0.1 \\ f(4)=0.2 \end{matrix}}\)
r把X转换成Y
\({\large \begin{matrix} r(0)=2 \\ r(1)=1 \\ r(2)=2 \\ r(3)=1 \\ r(4)=5 \end{matrix}}\)
Y值的分布。和为1。
\({\large \begin{aligned} & g(1)=f(1) + f(3) = 0.3 \\ & g(2)=f(0) + f(2) = 0.5 \\ & g(5)=f(4)=0.2 \\ \end{aligned}}\)
把Y转回X是\({\Large r^{-1}(Y)}\)
可总结出公式
\({\Large g(y)=\sum_{x\in r^{-1}(y)}f(x)}\)
\({\large x\in r^{-1}(y)}\)意思是多个x可能映射到同个y,那么从y返回去就是一个x集合。所以是一个和的形式。
对于连续的f。就是积分了。
\({\Large g(y)=\int_{r^{-1}(y)}f(x)dx}\)
把所有y对应的x的f(x)积起来。
\({\Large g(y)}\)即是Y的pdf,所有\({\Large g(y)}\)值的和为1。
pdf是针对某个y值,如果把y值扩展为从\(-\infty\)开始,就变成cdf。
\({\Large G(y)=\int_{r^{-1}(-\infty,y)}f(x)dx}\)
这时如果规定r函数xy一一对应并且单调递增,那么r的反函数可以形成一个正常的积分范围。
\({\large \begin{matrix} r(0)=2 \\ r(1)=3 \\ r(2)=4 \\ r(3)=7 \\ r(4)=18 \end{matrix}}\)
可以体会到,一一对应并且单调递增的效果就是把映射做成有序并严格隔离。这样两个cdf就能相等。
\({\Large G(y)=F(r^{-1}(y))}\)
两边微分cdf得pdf
\({\LARGE g(y)=f(r^{-1}(y))\frac{d}{dy}(r^{-1}(y))}\)
如果r是单调递减,有
\({\Large G(y)=1-F(r^{-1}(y))}\)
\({\LARGE g(y)=-f(r^{-1}(y))\frac{d}{dy}(r^{-1}(y))}\)
如果r递减,有
\({\Large \frac{d}{dy}(r^{-1}(y)) \lt 0 }\)
可以把前面的负号拿到后面。递增递减的两个\({\Large g(y)}\)可以统一写成
\({\LARGE g(y)=f(r^{-1}(y))|\frac{d}{dy}(r^{-1}(y))|}\)
又\({\Large r^{-1}(y) = x}\)。最终
\({\LARGE g(y)=f(x)|\frac{dx}{dy}|}\)
13.5.1 多维的变换#
涉及多重积分的换元。见[THOMAS' CALCULUS]14.8。
有的积分难算,可以尝试替换变量,实际就是换一个坐标系,变得容易算。
单变量的替换:
\({\LARGE \int_{g(a)}^{g(b)} f(x)dx=\int_{a}^{b}f(g(u))g'(u)du }\)
其实是多变量的特殊形式。
Jacobian。\({\LARGE J(u, v) = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial x}{\partial v} \end{vmatrix}}\)
最终的转换
\({\LARGE \iint_{R} f(x,y)dxdy=\iint_{G}f(g(u,v), h(u, v))J(u, v)dudv }\)
[THOMAS' CALCULUS]里的例子。Jacobian的一维转换特例。\({\LARGE g(y)=f(x)|J_x(y)|}\)
13.5.2 极坐标的转换#
\({\Large \left \{\begin {aligned} & x=r cos\phi \\& y=rsin\theta \end{aligned}\right.}\)
\({\Large J(r, \theta) = \begin{vmatrix} cos\theta & -rsin\theta \\ sin\theta & rcos\theta \end{vmatrix}}\)
\({\Large =r(cos^2\theta + sin^2\theta )}\)
\({\Large =r}\)
所以
\({\Large p(r, \theta)=r p(x, y)}\)
13.5.3 球面坐标的转换#
\({\Large \left \{\begin {aligned} & x=rsin\theta cos\phi \\& y=rsin\theta sin\phi \\& z=rcos\theta \end{aligned}\right.}\)
\({\Large J(r, \theta, \phi) = \begin{vmatrix} sin\theta cos\phi & rcos\theta cos\phi & -rsin\theta sin\phi\\ sin\theta sin\phi & rcos\theta sin\phi & rsin\theta cos\phi\\ cos\theta & -rsin\theta & 0 \end{vmatrix}}\)
\({\Large =r^2(sin\theta cos^2\theta cos^2\phi + sin^3\theta sin^2\phi + sin\theta cos^2\theta sin^2\phi + sin^3\theta cos^2\phi)}\)
\({\Large =r^2(sin\theta cos^2\theta + sin^3\theta )}\)
\({\Large =r^2sin\theta}\)
所以笛卡尔坐标系xyz上某个区域A的积分可转成球面坐标系对应的B区域的积分
\({\Large \iiint_AF(x,y,z)dxdydz=\iiint_BG(r, \theta,\phi)(r^2sin\theta)drd\theta d\phi}\)
对于pdf有
\({\Large p(r,\theta, \phi) = p(x,y,z)r^2sin\theta}\)
\({\Large dw= sin\theta d\theta d\phi}\)
那么对于半球上的积分
\({\Large \int p(w)dw=\int p(\theta,\phi)d\theta d\phi = 1}\)
把\({\Large dw}\)代入得
\({\Large \int sin\theta p(w) d\theta d\phi = \int p(\theta,\phi)d\theta d\phi}\)
所以
\({\Large sin\theta p(w)=p(\theta,\phi)}\)
这样也能从对于立体角的pdf转成对于极坐标的pdf。
13.6 多维变换的2d采样#
对于不可拆分的密度函数,要从\({\Large p(x, y)}\)里求marginal density function。
\({\Large p(x)=\int p(x, y)dy}\)
看做只针对x的密度函数。实际这是每个x,在所有y上的平均密度。
概率上有
\({\LARGE p(y|x)=\frac{p(x, y)}{p(x)} }\)
所谓的conditional density function。
marginal density function\(p(x)\),对\(p(x)\)采样出X。这样就把2d采样转成了两个分开的1d采样。
13.6.1 对半球均匀采样#
那么因为pdf积分为1
\({\Large \int_{H^2} p(w)dw = 1}\)
\({\Large C\int_{H^2} dw = 1}\)
半球范围的立体角和为\(2\pi\)
\({\Large C2\pi = 1}\)
所以
\({\Large p(w)=\frac{1}{2\pi}}\)
[[#13 5 3 球面坐标的转换]] 里有
\({\Large sin\theta p(w)=p(\theta,\phi)}\)
所以
\({\Large p(\theta,\phi)=\frac{sin\theta}{2\pi}}\)
这个例子对\((\theta,\phi)\)采样是可分开的,但是用上一节的marginal density function也是可以求的。
对\(\phi\)积分
\({\Large p(\theta) = \int_{0}^{2\pi} \frac{sin\theta}{2\pi} d\phi=sin\theta}\)
\({\LARGE p(\phi|\theta)=\frac{p(\theta,\phi)}{p(\theta)} = \frac{1}{2\pi}}\)
有了pdf,按[[#13 3 1 INVERSION方法]]采样。
\({\Large P(\theta)=\int_{0}^{\theta}sin\theta'd\theta' = -cos\theta|_{0}^{\theta} = 1-cos\theta}\) (积分得到cdf)
\({\Large 1-cos\theta = \xi_1}\) (给定随机值反算变量)
\({\Large \theta = acos(1- \xi_1)}\) (完成采样)
\({\Large P(\phi|\theta) = \int_{0}^{\phi} 1/2\pi d\phi' =\phi/2\pi|_{0}^{\phi}=\phi/2\pi }\) (积分得到cdf)
\({\Large \phi/2\pi = \xi_2}\) (给定随机值反算变量)
\({\Large \phi = 2\pi\xi_2}\) (完成采样)
最终转到笛卡尔坐标系即球面上的xyz
\({\Large \begin {aligned} & x=rsin\theta cos\phi =r\sqrt {1-(1-\xi_1)^2} cos(2\pi\xi_2) \\& y=rsin\theta sin\phi =r\sqrt {1-(1-\xi_1)^2} sin(2\pi\xi_2) \\& z=rcos\theta=r(1-\xi_1) \end{aligned}}\)
到这里可以看到,对一个半球均匀采样,乍看很简单,实际包含大量推导。
13.6.2 对单位disk采样#
对disk采样看上去简单,对半径采样再对角度采样,实际不对。见图13.10。
针对圆形均匀采样,从面积的角度来看,采样是均匀的,采到每个单位面积的概率为
\({\Large p(x,y)=\frac{1}{\pi R^2}}\)
我呢保留R,要注意不能写成r,容易跟后面的变量r搞混。要把R看成常数。
根据13.5.2进行极坐标的转换
\({\Large p(r, \theta)=\frac{r}{\pi R^2}}\)
算marginal density,对\(\theta\)积分
\({\Large p(r)=\int_{0}^{2\pi}\frac{r}{\pi R^2}d\theta = \frac{2r}{R^2}}\)
算conditional densities
\({\Large p(\theta|r) = \frac{p(r, \theta)}{p(r)} = \frac{1}{2\pi} }\) (是一个常数)
积分得cdf并采样
\({\Large P(r)=\frac{r^2}{R^2} = \xi_1}\)
\({\Large r=R\sqrt{\xi_1}}\)
\({\Large P(\theta|r)=\frac{\theta}{2\pi} = \xi_2}\)
\({\Large \theta=2\pi\xi_2}\)
虽然实现了disk的均匀采样,但是上述方法对disk有distortion。13.8.3节讲了它的坏处。
一个较好的方法是concentric mapping。
13.7 RUSSIAN ROULETTE#
[Realistic Image Synthesis Using Photon Mapping]另外最完美的迭代次数是无穷大,这也不现实。
Russian roulette可以设置终止条件,按概率去终止一些不想要的计算,同时还能保证结果无偏(unbiased)。
首先有期望值的定义
\({\Large E[X]=\sum_{i=1}^{n}x_ip(x_i)}\)
这时可以做一个概率q,算一个\(beta'\)作为新的beta。
\({\Large beta' =\begin{cases} \frac{1}{q} beta & (概率q) \\ 0 & (概率1-q) \end{cases} }\)
q是完全可以自定义的,比如当beta小于0.2时,我决定此时得有0.1的概率不要再继续弹射了,也就是让\(beta'\)返回0。这时q取0.9。
然后我们可以写代码。当beta小于0.2时,取一个[0, 1]随机数,如果大于0.1,继续迭代。否则终止,也就是后续的贡献取0。
为什么是\({\Large \frac{1}{q} beta}\)?简单计算一下,原始正确值是beta。我们按概率来看,进行10次操作,会有9次返回\({\Large \frac{1}{q} beta}\),1次返回0。
那么10次操作
\({\Large 平均值 = \frac{\frac{beta}{0.9} \times 9 + 0\times 1}{10}=beta}\)
本质上就是利用概率,随机终止操作,同时保证beta的期望值不变,即无偏。
\({\Large E[beta'] = \frac{1}{q} beta \times q + 0 \times (1-q)}\)
\({\Large = beta = beta \times 1 = E[beta]}\)
13.10 重要性采样#
重要性采样是减小方差的好工具
对于这个蒙特卡洛估算子
\({\Large F_N=\frac{1}{N} \sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}}\)
如果选的p(x)与f(x)图形越相似,方差就越小,收敛速度越快。
假设
\({\Large p(x) = cf(x)}\)
那么
\({\Large \int p(x)dx = \int cf(x)dx = 1}\)
\({\Large c = \frac{1}{ \int f(x)dx}}\)
这时估算子里
\({\Large \frac{f(X_i)}{p(X_i)} = 1/c = \int f(x)dx}\)
正好已经得到了答案,方差为0。
这个是完美的假设,完全不实用。但如果能找到近似的p(x),是能减小方差的。
14 光的传播1-表面反射#
直接光的积分
\({\Large L_o(p, w_o)=\int_{S^2} f(p, w_o, w_i)L_i(p, w_i)|cosθ_i|dw_i}\)
但这个积分一般是没法正常算的。用蒙特卡洛方法能得出近似结果。
\({\LARGE L_o(p, w_o) ≈ \frac{1}{N} \sum \frac{f(p, w_o, w_i)L_i(p, w_i)|cosθ_i|}{pdf(w_i)}}\)
14.1 对反射函数采样#
BxDF::Pdf()
14.1.1 微小面采样#
Sample_wh()是从\({\Large \omega_{o}}\)随机采样出一个normal\({\Large \omega_{h}}\)。
\({\Large \theta_{h}}\)是\({\Large \omega_{h}}\)和Z轴之间的夹角。
各向同性Beckmann为例
\({\LARGE D(\omega_h)=\frac{e^{-tan^2\theta_h/\alpha^2}}{\pi\alpha^2cos^4\theta_h}}\)
\({\LARGE \xcancel{ p(\theta_h)=\frac{e^{-tan^2\theta_h/\alpha^2}}{\pi\alpha^2cos^4\theta_h}}}\)
续
到这里必须看懂13章里的各种转换和采样。之前没有仔细看13章,所以这里搞不懂。
由[[#8 4 2 微小面分布函数]] 规定
\({\LARGE \int_{H^2}D(\omega_h)cos\theta_hd\omega_h=1 }\)
\(D(w_h)\)并不是一个标准的pdf。pdf需要计算。
\({\LARGE \int_{H^2}D(\omega_h)cos\theta_hd\omega_h=1 = \int_{H^2}p(\omega_h)d\omega_h}\)
\({\LARGE D(\omega_h)cos\theta_h= p(\omega_h)}\)
\({\LARGE p(\omega_h) = \frac{e^{-tan^2\theta_h/\alpha^2}}{\pi\alpha^2cos^3\theta_h} }\)
[[#13 5 3 球面坐标的转换]] 里有
\({\Large sin\theta p(w)=p(\theta,\phi)}\)
所以
\({\LARGE p(\theta,\phi) = \frac{sin\theta e^{-tan^2\theta_h/\alpha^2}}{\pi\alpha^2cos^3\theta_h} }\)
\({\Large p(\theta, \phi) = p(\theta)p(\phi)}\)
其中\({\Large p(\phi)=1/2\pi}\)
所以
\({\LARGE p(\theta) = \frac{2sin\theta e^{-tan^2\theta_h/\alpha^2}}{\alpha^2cos^3\theta_h} }\)
\({\Large -e^{-tan^2\theta/\alpha^2}|_{0}^{\theta} = 1-e^{-tan^2\theta/\alpha^2} =\xi}\)
\({\Large tan^2\theta=-\alpha^2ln(1-\xi)}\)
\(\phi\)是独立的圆周上的均匀分布,\({\Large p(\phi)=1/2\pi}\),所以
\({\Large \phi=2\pi\xi}\)
到此完成了各向同性Beckmann采样。
各向同性GGX
\({\LARGE D(\omega_h)=\frac{\alpha^2}{\pi cos^4\theta_h(\alpha^2+tan^2\theta_h)^2}}\)
\({\LARGE p(\omega_h)=\frac{\alpha^2}{\pi cos^3\theta_h(\alpha^2+tan^2\theta_h)^2}}\)
\({\LARGE p(\theta, \phi)=\frac{sin\theta \alpha^2}{\pi cos^3\theta_h(\alpha^2+tan^2\theta_h)^2}}\)
\({\LARGE p(\theta)=\frac{2sin\theta \alpha^2}{cos^3\theta_h(\alpha^2+tan^2\theta_h)^2}}\)
\({\Large \frac{\alpha^2}{(\alpha^2 - 1)((\alpha^2-1)cos^2(t)+1)}|_{0}^{\theta} = \frac{\alpha^2}{(\alpha^2 - 1)((\alpha^2-1)cos^2(\theta)+1)}-\frac{1}{\alpha^2 - 1} = \xi}\)
最终采样
\({\Large cos^2\theta = \frac{1-\xi}{\alpha^2 \xi-\xi+1}}\)\({\Large \phi=2\pi\xi}\)
14.1.2 FresnelBlend#
14.1.3 镜面反射和传输#
14.1.4 傅立叶bsdf#
14.1.5 例子:估算反射率#
14.1.6 BSDF::Sample_f()#
14.2 对光源采样#
Light::Sample_Li()
14.2.4 infinite area light#
环境map,一般情况不同方向的光差别巨大。
波动越小越好。图14.10做对比。波动越大noise越多。
14.3 直接光#
14.4 光的传输方程/渲染方程#
14.4.1 基本推导#
先有直接光的积分
\({\Large L_o(p, w_o)=\int_{S^2} f(p, w_o, w_i)L_i(p, w_i)|cosθ_i|dw_i}\)
p点在\(w_o\)方向射出的光能,为所有光打到p点,进行brdf计算后,在\(w_i\)方向的总和。
\({\Large L_o(p, w_o)=L_e(p, w_o) + \int_{S^2} f(p, w_o, w_i)L_i(p, w_i)|cosθ_i|dw_i}\)
设点p2为\(t(p, wi)\),有
\({\Large L_i(p, w_i) = L_o(t(p, w_i), -w_i)}\)
替换进渲染方程得到最终形态。方程14.13
\({\Large L_o(p, w_o)=L_e(p, w_o) + \int_{S^2} f(p, w_o, w_i)L_o(t(p, w_i), -w_i)|cosθ_i|dw_i}\)
14.4.2 LTE的解析解#
14.4.3 基于面的LTE方程#
渲染方程14.13其实相对复杂,原因是场景中的几何体的关系隐藏在\(t(p, w_i)\)中。
如果把这个式子做成显式会更好。
\({\Large E(p, n) = ∫Li(p, w)|cos\theta|dwi}\)
\({\Large dw = cos\theta_o dA/r^2}\)
\({\Large E(p, n) = ∫La |cos\theta_i| cos\theta_o dA/r^2}\)
假设3个点。光从p3打到p2再打到p。
定义p2到p的光能为\(L(p2 \top)\)
bsdf函数,\(f(p2, w_o, w_i)\),可以写成 \(f(p3 \to p2 \to p)\)。
做一个G函数
\({\Large G(p \leftrightarrow p2) = V(p \leftrightarrow p2) \frac{ |cos\theta_i||cos\theta_o| }{|p-p2|^2}}\)
其中V为两点是否相互可见。如果不可见返回0。
做替换,\(dw\)转为\(dA\)。
最后渲染方程14.13变为14.15
\({\Large L(p2 \to p) = Le(p2 \top) + ∫ f(p3 \to p2 \to p) L(p3 \to p2) G(p3 \leftrightarrow p2) dA(p3)}\)
积分范围是场景内所有的面(所有的p3对应的面)。
原始的反射是对所有立体角积分。现在转成了对场景内所有的微小面积分。
14.4.4 对path积分#
有了方程14.15。可以推出更灵活的LTE,包含path信息,能延伸到更高维的path空间。
对于程序来说可以做成显式的积分,更好处理,而不是最初的较笨拙的递归形式。
设4个点p0/p1/p2/p3。p0为相机。有
把式子拉长、对齐,更直观。
L(p1->p0) = Le(p1->p0)
+ ∫ L(p2->p1) f(p2->p1->p0) G(p2<->p1) dA(p2)
展开L(p2->p1)
= Le(p1->p0)
+ ∫ (Le(p2->p1) + ∫ L(p3->p2) f(p3->p2->p1) G(p3<->p2) dA(p3)) f(p2->p1->p0) G(p2<->p1) dA(p2)
把展开得到的Le项和∫分别乘出来
= Le(p1->p0)
+ ∫ Le(p2->p1) f(p2->p1->p0) G(p2<->p1) dA(p2)
+ ∫ ∫ L(p3->p2) f(p3->p2->p1) G(p3<->p2) dA(p3) f(p2->p1->p0) G(p2<->p1) dA(p2)
再展开
= Le(p1->p0)
+ ∫ Le(p2->p1) f(p2->p1->p0) G(p2<->p1) dA(p2)
+ ∫ ∫ Le(p3->p2) f(p3->p2->p1) G(p3<->p2) dA(p3) f(p2->p1->p0) G(p2<->p1) dA(p2)
+ ∫ ∫ ∫ L(p4->p3) f(p4->p3->p2) G(p4<->p3) dA(p4) f(p3->p2->p1) G(p3<->p2) dA(p3) f(p2->p1->p0) G(p2<->p1) dA(p2)
可无限次展开,每次展开就是多一次光的弹射。
可发现规律
每次展开会多出一项,下一层的Le乘上层的最末项(除去本身)。
并把最末项(除去本身)增加一重反射积分。
代码实现#
把L分成直接光和间接光。
∫ L(p4->p3) f(p4->p3->p2) G(p4<->p3) dA(p4)
采样出来的path,在蒙特卡洛的思想中,就代表了打到场景中所有的物体的面的path,也就是近似得到了所有的间接光。
到此已经实现了全局光照!
14.5 路径追踪#
一些细节解释
15 光的传播2-体渲染#
[Realistic Image Synthesis Using Photon Mapping]学了光子映射。15.1 传输方程#
传输方程是光在介质中传输的核心。
上一章的光的传输方程其实是传输方程的特例,省略了介质的影响。
首先对于任何能量的衰减,都有微分方程
\({\Large L'(s) = -\sigma(s) L(s)}\)
s是移动的距离,解得
\({\LARGE L(s) = L(0) e^{-\int_{0}^{s}\sigma(t)dt}}\)
\({\LARGE T_r(s) = e^{-\int_{0}^{s}\sigma(t)dt}}\)
这个在pbrt叫做beam transmittance,有的叫做optical depth。对任何能量都适用。
再回到问题,介质中某\({\Large (p, \omega)}\)上总的能量增加为介质发光(Le) + (in-scattering),对于任何一点p都可以采样计算。
\({\Large L_{gain}(p, \omega) = L_e(p, \omega) + \sigma_s(p, \omega) \int_{S^2}^{}p(p, \omega', \omega)L_i(p,\omega')d\omega'}\)
那么p和p0之间的所有点对p的能量贡献为
\({\Large L_i(p, \omega) = \int_{0}^{s} T_r(s') L_{gain}(p', \omega)ds'}\)
\({\Large L_i(p, \omega) = \int_{0}^{s} T_r(s') L_{gain}(p', -\omega)ds' + T_r(s)L_o(p_0, -\omega)}\)
再回头看看体渲染方程
\({\LARGE L(s) = \int_{0}^{s} e^{-\int_{t}^{s}p(t')dt'} q(t)dt + L(0)e^{-\int_{0}^{s}p(t')dt'} }\)
惊人的相似。可以说本质上完全一致!
15.2 采样#
15.2.1 均匀介质#
transmittance,距离和衰减比例的关系。\({\LARGE T_r(s) = e^{-\int_{0}^{s}\sigma(t)dt}}\)
只考虑均匀介质有
\({\Large T_r(s) = e^{-\sigma s}}\)
s初始0时值为1,无穷大时值为0。
13.3章算过了对这种函数的采样
\({\Large X = -\frac{ln(1-\xi)}{\sigma}}\)
同时normalize后的pdf函数为
\({\Large pdf(s) = \sigma e^{-\sigma s}}\)
那么就可以得到0到s的衰减值的蒙特卡洛积分了。
这也是[Realistic Image Synthesis Using Photon Mapping]10.4.1里讲的Adaptive Ray Marching
期望值:
\({\Large E[X] = \int_{0}^{\infty} x\cdot pdf(x)dx}\)
根据[托马斯微积分]第8.2的Integration by Parts方法
\({\Large \int_{a}^{b} uv'dx = uv|_{a}^{b}-\int_{a}^{b} vu'dx}\)
那么
\({\Large E[X] = \int_{0}^{\infty} s\cdot pdf(s)ds}\)
\({\Large = \int_{0}^{\infty} s(\sigma e^{-\sigma s})ds}\)
\({\Large = (-se^{-\sigma s})|_{0}^{\infty} - \int_{0}^{\infty} -e^{-\sigma s}\cdot 1 ds}\)
\({\Large = (-se^{-\sigma s})|_{0}^{\infty} - \frac{ e^{-\sigma s}}{\sigma}|_{0}^{\infty}}\)
\({\Large = \frac{1}{\sigma}}\)
\({\Large L_i(p, \omega) = \int_{0}^{s} T_r(s') L_{gain}(p', -\omega)ds' + T_r(s)L_o(p_0, -\omega)}\)
再对transmittance采样出距离,分两种情况。tMax左边和右边。
如果距离落在tMax之外#
就相当于跳过了两点之间的所有中间点。只需计算L0也就是p0的能量,带上衰减。
\({\Large pdf(s) = \sigma e^{-\sigma s}}\) (normalize后)
从0开始到某个s的积分
\({\Large \int_{0}^{s} \sigma e^{-\sigma s'}ds' = -e^{-\sigma s}|_{0}^{s} = 1 - e^{-\sigma s}}\)
那么从x到无穷大的积分就是用1减它
\({\Large pdf = e^{-\sigma s} = Tr}\)
如果距离落在tMax之内#
采样值为Tr,pdf为\(\sigma\)Tr。同样pdf要做平均。
另外考虑in-scattering的系数
\({\Large L_i(p, \omega) = \int_{0}^{s} T_r(s') L_{gain}(p', -\omega)ds}\)
\({\Large L_{gain}(p, \omega) = L_e(p, \omega) + \sigma_s(p, \omega) \int_{S^2}^{}p(p, \omega', \omega)L_i(p,\omega')d\omega'}\)
忽略自发光Le。Sample函数返回的Beta值要再乘\({\Large \sigma_s}\)。
这样就完成了各向同性介质的采样函数HomogeneousMedium::Sample
数学问题#
以后再研究。
15.2.3 对phase函数采样#
\({\LARGE p(\theta, \phi) = \frac{1-g^2}{4\pi(1+g^2-2gcos\theta)^{1.5}}}\)
首先对于立体角积分,它本质是有两个变量,因为和\(\phi\)无关所以可以简写。
\({\LARGE p(\theta) = \frac{1-g^2}{4\pi(1+g^2-2gcos\theta)^{1.5}}}\)
\({\Large \int_{0}^{2\pi } \int_{0}^{\pi } p(\theta) sin\theta d\theta d\phi = 1}\)
\({\Large \int_{0}^{\pi } p(\theta) sin\theta d\theta = 1 / 2\pi}\) (\(\phi\)无关,可以分开算出来)
\({\Large \int_{0}^{\pi } \frac{1-g^2}{4\pi(1+g^2-2gcos\theta)^{1.5}} sin\theta d\theta = 1 / 2\pi}\)
\({\Large \int_{1}^{-1 } - \frac{1-g^2}{4\pi(1+g^2-2gu)^{1.5}} du = 1/2\pi}\)
处理负号
\({\Large \int_{-1}^{1 } \frac{1-g^2}{4\pi(1+g^2-2gu)^{1.5}} du = 1/2\pi}\)
(到这里其实可以算积分,验证这个积分值是否正确,也就是验证这个phase函数的cdf是否为1。我是在后面算出积分时验证了一下,是对的。)
这其实已经到了inversion方法的求积分步骤
\({\Large \int_{-1}^{1 } p(u) du = 1/2\pi}\)
本质仍然是对原函数采样,不过变量换成了\(u=cos\theta\),那么采样出来的值就是\(cos\theta\)。积分域也发生变化。
仍然需要做normalize。 因为右边是确定的值,所以可以直接除成1。
\({\Large \int_{-1}^{1 } \frac{1-g^2}{2(1+g^2-2gu)^{1.5}} du = 1}\)
这样做好了准备工作,按inversion方法求导。
\({\Large cdf(u)=\int_{-1}^{u} pdf(u')du'}\)
要注意是从-1开始积分!
\({\Large cdf(u)=\int_{-1}^{u} \frac{1-g^2}{2(1+g^2-2gu')^{1.5}}du'}\)
\({\Large cdf(u)= \frac{1-g^2}{2g\sqrt{1+g^2-2gu'}}|_{-1}^{u}}\)
\({\Large cdf(u)= \frac{1-g^2}{2g\sqrt{1+g^2-2gu}} - \frac{1-g}{2g}}\) (这里可以验证一下,u取1时,确实积分为1)
\({\Large cdf(u) + \frac{1-g}{2g} = \frac{1-g^2}{2g\sqrt{1+g^2-2gu}}}\)
\({\Large \sqrt{1+g^2-2gu} = \frac{1-g^2}{2g(cdf(u) + \frac{1-g}{2g})}}\)
\({\Large 1+g^2-2gu = (\frac{1-g^2}{2g(cdf(u)) + 1-g})^2}\)
得到反函数
\({\Large u = \frac{1}{2g}( 1+g^2- (\frac{1-g^2}{2g(cdf(u)) + 1-g})^2)}\)
采样
\({\Large cos\theta = \frac{1}{2g}( 1+g^2- (\frac{1-g^2}{2g\xi_1 + 1-g})^2)}\)
\({\Large \phi = 2\pi\xi_2}\)
其他参考
15.3 体光传输#
16 光的传播3-双向方法#
16.1#
16.2 STOCHASTIC PROGRESSIVE PHOTON MAPPING#
pbrt直接讲sppm,从理论开始讲,看不懂。先看别的专门讲光子映射的材料可能更容易。
[Realistic Image Synthesis Using Photon Mapping][Photorealistic Rendering using the PhotonMap][Advanced global illumination]光子映射属于粒子追踪算法。从光源开始。创建path,最终连到camera。
16.2.1 partical-tracing的理论基础#
直觉上比较简单,但问题也很多。比如能量如何衰减?cos项如何处理?
粒子追踪算法在场景中的点\(p_j\)生成N个样本的光照。
\({\Large (p_j, \omega_j, \beta_j)}\)
给定importance function \(W_e(p, \omega)\)。
。。。
17 总结与展望#
资源/参考#
[Physically Based Rendering][THOMAS' CALCULUS][Real-Time Rendering][Fundamentals of Computer Graphics][Mathematics for Computer Graphics][3D Math Primer for Graphics and Game Development][Mathematics for 3D Game Programming and Computer Graphics][Introduction to Probability Models][A FIRST COURSE IN PROBABILITY][Realistic Image Synthesis Using Photon Mapping]
[Advanced global illumination]
[Accuracy and Stability of Numerical Algorithms]
[Ray Tracing Deformable Scenes Using Dynamic Bounding Volume Hierarchies]
ROBUST MONTE CARLO METHODS FOR LIGHT TRANSPORT SIMULATION
[A Practical Guide to Global Illumination using Photon Maps]
Vulkan学习#
如果api报错,得把validation layer整上。有些不会导致崩溃的错误也能显示出来。
常见错误是某个配置里数量填了非0,但指针填了nullptr。
画三角形大概要一千行代码。包含基本的vulkan流程和概念。
[Learning Vulkan]#
每个family提供。。???
queue被驱动按提交顺序读取。
app的职责#
- 为command的执行做准备比如准备各种resource,编译shader。设置render状态。创建pipeline。draw call。
- 管理memory
- 同步
异常处理
queue#
app要确保把cb提交到正确的queue。
event
fence
pipeline barrier
object model#
app层面。各种实例,比如device,queue,cb等等都称为object。
api层面,object以handle来识别。
dispatchable handle
non-dispatchable handle
object生命周期#
app必须负责创建和销毁。
vulkan app的结构#
硬件初始化#
Window presentation surfaces#
wsi可看作display和app之间的接口。
resource setup#
分配内存expensive。所以要先分配内存再suballocate objects。
pipeline setup#
Descriptor sets and descriptor pools#
Shaders with SPIR-V#
Pipeline management#
Recording commands#
Queue submission#
code#
vkEnumerateInstanceLayerProperties // 可选 if (settings.validation)
vkCreateInstance
vkEnumeratePhysicalDevices
vkGetPhysicalDeviceSurfaceSupportKHR
vkCreateSwapchainKHR
vkCreateImageView
vkCreateFramebuffer
vkCreateCommandPool
vkAllocateCommandBuffers
ImGui::CreateContext();