B树的C++实现#
简介#
https://en.wikipedia.org/wiki/B-tree
B树也属于平衡树,空间复杂度O(n),查询/插入/删除的时间复杂度都是O(log(n))。 适用于大块数据的存储操作,相比其他树型结构可以降低很多磁盘io,广泛用于数据库和文件系统。是一些更高级算法的基础。
knuth的定义(The art of computer programming)#
一棵m阶B树(a btreee of order m)
每个节点最多有m个子节点。
除了根和叶子,每个节点至少有m/2个子节点。
根最少有2个子节点,除非它也是叶子。
所有叶子都在同一层上,且不包含具体数据。
每个有k个子节点的非叶子节点,都包含k-1个key。
其他性质或情景#
目的是存大量的key。可以快速增删查某个key。
规定不存在重复的key
实际应用中一个节点可能包含上千个key。key对应的数据也存在同个节点,这里我们忽略数据,只看key。
如果树的节点总数为n,那么树的高度为O(log(n))这个级别,就是说高度和节点总数为对数关系,所以高度相对会很低。 做成图像的话,与其他树型结构相比,是一棵矮胖的树。
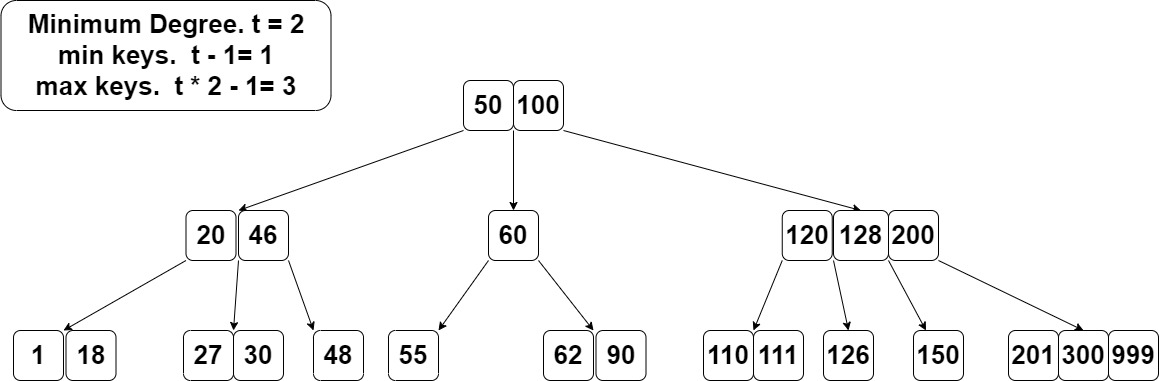
先简单观察一个例子,这棵B树存了一系列数字。 根存2个key 50,100,有3个子节点。 key其实充当分隔的角色,n个key可以把数据范围分隔成n+1段,对应n+1个子节点。 搜索时就按这个分隔来。比如搜索27。50和100把数分割成三段,27落在第一段,那么对应[20,46]这个子节点。又落在中间一段,那么走到[27, 30]。(要判断一下作为分割者的key,比如搜20的话,走到[20, 46]时直接就找到了) 这样已经走到叶子[27, 30],找到27。 如果叶子里找不到,就是不存在。
为什么B树可以降低磁盘io#
一般把系统存储实体分为主副两块(primary/secondary),简单对应就是内存和硬盘。
读写硬盘比读写内存慢了多个数量级,因为硬盘读写包含了机械操作,类似唱片机。 读一个地址需要转动,定位,一套操作下来,相同的时间内可能可以读写内存上万次。 读磁盘数据时按页来的,典型是2k到16k字节。
按上述情况,从磁盘读一块数据比用cpu处理这块数据慢得多。 那么可考察两个值:
磁盘io次数
cpu计算时长
磁盘io次数可看成一次磁盘读或写数据的总页数。 这里不是绝对精确,因为每次磁盘读写耗时不一定是一样的,机械臂移动的距离不一样。 但总体对比仍是准确的。
一个典型的B树应用中,数据量是非常大的,不是所有数据都能装到内存里。 B树算法只会按需把数据页放到内存,在内存中保留固定页数的数据。这样B树不会受一台计算机的内存大小限制。
可以这样对数据操作来建模,x表示一个逻辑物体,磁盘读(x)表示从磁盘读这个物体的数据,磁盘写(x)表示往磁盘写入这个物体的数据。 那么典型的对x的一次读写操作可以表示成
准备读x
磁盘读(x)
cpu处理x在内存中的数据
磁盘写(x)
其他内存操作
因为磁盘读(x)和磁盘写(x)占了耗时的大部分,且不可避免,所以得让一次磁盘操作尽量多处理数据。 那么在实际算法中得体现就是,一个节点中key的数量很大,实用中通常取值50到2000。 因为是树型指数级的关系,节点分叉数的微小增长就能快速减小整个树的高度,也就是减小了搜索次数,也就是减小了读磁盘的次数。 例如每个节点存1000个key,只需3层就能存1002001000(10亿)个key。
<<算法导论>>的定义#
每个节点x的属性
节点存有x.n个key
key以非降序排列。即x.key1 <= x.key2 …. <= x.key(x.n)
x.leaf标识是否为叶子,非叶子节点又称为内部节点(internal node)
每个内部节点x存有x.n+1个类指针数据c(x.c1,x.c2 … x.c(x.n+1)),每个指向对应的下一层节点。 叶子没有下一层,不存指针。
节点里的key把key空间分割成k.n+1份。c其实就对应被key分割出来的n+1个范围。
所有叶子的高度相同,即树的高度。
节点有key的高低数量限制。定义一个大于等于2的值t,为B树的最小度(minimum degree)。其实就是knuth定义里的阶除以2。这里用minimum degree,不用除法,感觉舒服一些。
除了根,所有节点至少含有t-1个key,即至少有t个子节点。 如果树不是空的,根至少得有1个key。
每个节点最多有2t-1个key。因此最多只能有2t个子节点。 如果节点有2t-1个key,就说它是满的(full)。
这个最小度(minimum degree)是实用时我们可调的参数。它限定了每个节点里的key数范围。
B树的操作#
两个约定#
B树的根节点总是已经在内存中,不需要磁盘读()操作。当根节点改变时,磁盘写()还是需要的。
所有函数的节点参数都必须已经进行过磁盘读()操作。
我按算法导论的流程来实现插入等操作,按wikipedia的流程实现删除操作。
搜索#
从节点x开始搜索k
btree_search(x, k):
if x.leaf:
return None
i = 1
while i <= x.n and k > x.key[i]:
i += 1
if i <= x.n and k == x.key:
return x, i
else:
磁盘读(x.c[i]
btree_search(x.c[i]], k)
和二分差不多
如果是叶子,说明没找到,返回None。
遍历当前节点的key,如果碰到相等的,说明找到了,直接返回节点和位置(x, i)。 如果碰到一个大于k的,k一定是落在这个key之前的分割范围内,对应c[i]]。 那么得先从磁盘读x.c[i]的数据,再往子节点搜索。 这里遍历可以改成二分查找。
设总结点数为N,那么搜索层数方面的复杂度是O(Log(t, N))。每层遍历的复杂度是O(t)。 整体CPU的耗时是O(tLog(t, N))。
初始化#
btree_create():
x = 分配新节点()
x.leaf = True
x.n = 0
磁盘写(x)
return x
初始化一个空的B树。O(1)磁盘操作和O(1)CPU时间。
插入key#
B树的插入比一般二叉树复杂,二叉树是直接添加一个叶子,B树是往节点添加一个key。 但B树的节点有容量限制。如果要往节点y插入key,但发现y满了(有2t-1个key),得找到中间的y.key[t],把它拿出来挪到y的父节点里,剩下的两边分成两个包含t-1个key的节点。
y挪到上层后把原来y对应的范围分割成两个范围,原来y节点分裂出来的两个新节点正好对应两个新范围。 这个操作叫分裂(
split)。即一个满的2t-1个key的节点拿出一个key放到父节点,再变成两个t-1的节点。
把分裂操作写成一个函数,对节点x的第i-1和第i个key之间对应的子节点进行分裂。
btree_split_child(x, i):
y = x.c[i] // 原来的子节点写为y
z = 分配新节点()
把y的后t-1个key复制到z
把y的第t个key插到x的i之前
z.n = t-1
y.n = t-1
x.n += 1
更新x的子节点的对应
磁盘写(y)
磁盘写(z)
磁盘写(x)
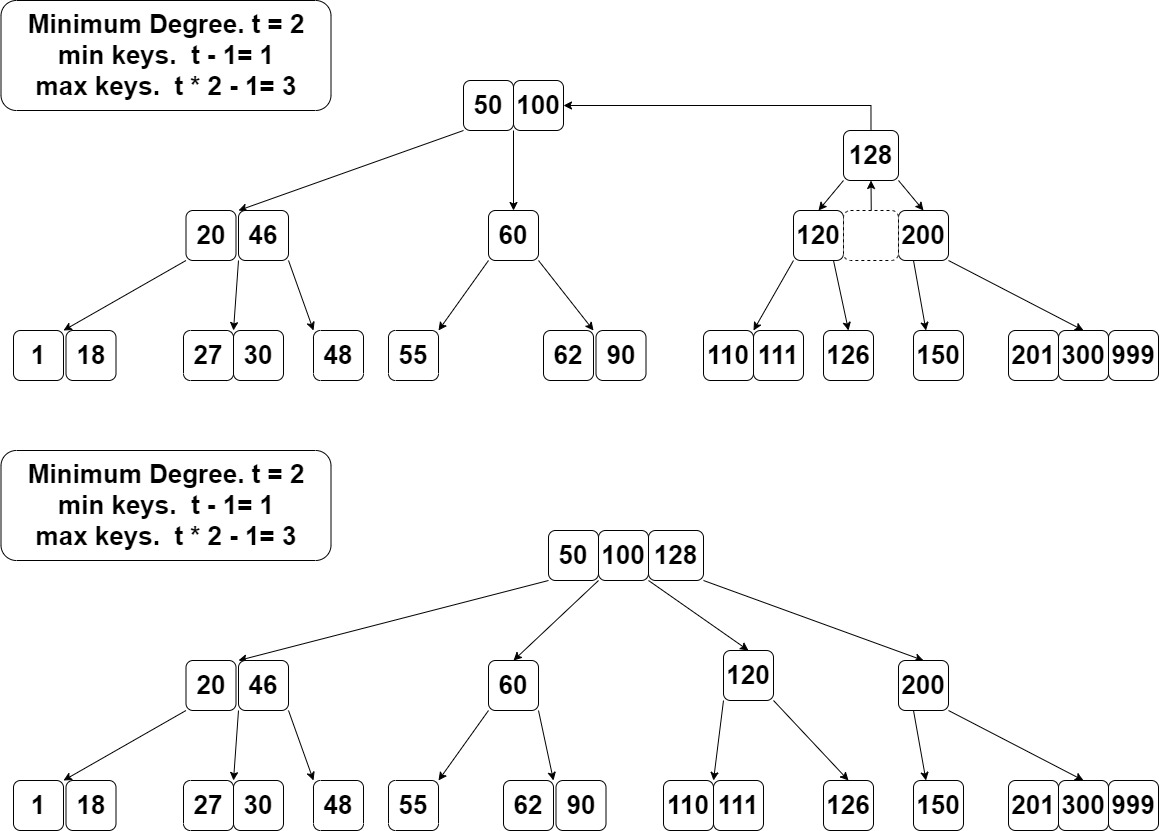
图中对[120, 128, 200]这个节点进行分裂。
问题来了,父节点会不会也是满的?不会。 插入操作是从顶层的根节点往下走,会不断检查子节点是不是满的,如果满了会先把它分裂。从而保证key数量不会超2t-1。 先不考虑根节点,做一个通用的插入函数。规定当前节点必须不是满的。
btree_insert_nonfull(x, k):
if x.leaf:
# 找到k的位置(第一个大于它的key之前,或末尾)插入
x.n += 1
# 磁盘写(x)
else:
# 同样找出插入位置i
# 磁盘读(x.c[i]) # 读出子节点数据
if x.c[i].n == 2t-1: # 如果已满,做分裂。
btree_split_child(x, i)
# 判断提上来的key,决定接下来往左还是往右走。
btree_insert_nonfull(x.c[i], k) # 往下走
如果是叶子,插入。 否则找到key所在的范围对应的子节点。 如果该子节点已满,先做分裂,再往左边的新子节点递归插入key。 如果没满,直接往子节点递归插入key。
完整的插入函数从根节点T开始。
btree_insert(T, k):
if T.n == 2t-1: # 根满了
s = 分配新节点()
T变为s的子节点
s变为根节点
btree_split_child(s, 1) # 原来的根节点作为子节点进行分裂
btree_insert_nonfull(新根节点, k)
可发现B树的高度只在根节点分裂时才+1。原来的根分裂成两个节点,中间的key提上去变成新的根。
key最终都是插入到叶子节点。
操作过程始终要保证节点key数在t-1到2t-1之间的性质。
插入后key满是合法的,不用管。等下次插入时会进行split。
上述操作是one pass,即从上到下一遍完成。也可以先插入,再从下往上按需进行分裂,可能更容易理解,但效率稍低。
删除一个key#
先找到key。如果存在的话,删除key,并保证树仍然满足B树的key数限制。
有两种策略,与插入类似。一是从根开始一遍完成,二是先找到要删除的key,再按情况重构(rebalance)使它维持平衡。这里用第二种,较直观。
先找到key所在节点
如果是叶子节点
从节点删除key
如果剩余key数大于等于t-1,返回成功。
否则进行rebalance
如果是内部节点
找到key左边子节点开始的子树里的最大key a,也就是子树右下角的key(必然是在最底层的叶子节点)。
如果key所在节点的key数大于t-1,可直接用a替代key即可。不用做其他操作。
否则可同样尝试右边子树,找右边子树的最小key。
如果都无法直接替换,就强行用左边的a来替换key,再从a原来的节点开始做rebalance。
rebalance一定是从叶子节点开始。通常是从同一层的兄弟节点取一个key。如果兄弟节点的key不够,需要做merge操作。 merge操作从父节点拉一个key下来,放在中间,和左右子节点的key合并。 会导致父节点减少一个key,这时如果父节点的key小于t-1,就得对父节点再做rebalance,这样形成一个递归的模式。有可能一直往上返到根节点才结束。
rebalance(节点n)
如果左边兄弟节点key数大于等于t-1。做一个顺时针旋转,把左边兄弟节点最大的key替换父节点的key,父节点原来的key挪到n的key打头位置。
如果左边不行,尝试右边的对称操作。
如果都不行,做merge。
把父节点的key接到左兄弟最右边,把n的所有key再接到最右边。
这时父节点就减少了一个key。如果key不够,rebalance(父节点)。
删除key图示#
重申一些性质:
稳定状态下(非操作中),一个节点可能是满的。
如果非叶子节点有n个key,那么一定有n+1个子节点。
叶子都在同一层。
根最少可以只有1个key
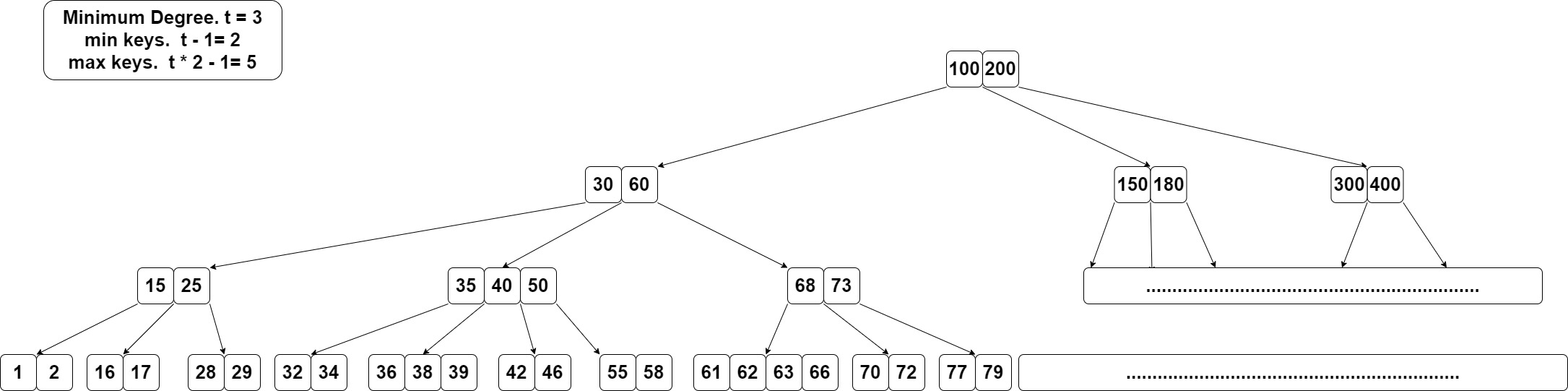
这个树minimum degree为3。那么非根节点的key数必须为2到5。
先搜索key
如果key在叶子
如果叶子key数大于t-1。例如图中的36、38、39、61、62、63、66,直接删除即可。
否则删除后走rebalance。
key在内部节点
比如删除40。左子树最大key为39,39所在节点key数大于t-1,可以直接把39挪到40的位置即可。
同样可以找右子树,比如删除35,用36替换即可。
又例如删除60,找右子树里的61替换即可。
如果左右的替换都会造成子节点key数不够,只能先强行替换,再走rebalance。 比如删除30,取29或32都会造成节点key数不够。那么选29替换,再对[28]这个节点做rebalance。
rebalance(节点n)
看左边兄弟节点,如果key数大于t-1,做顺时针旋转即可。
比如删除50后,46代替50,对剩下的42作rebalance,左边key有多余,拿出最末的39代替40,40转下来放到节点n的头部。
如果左边不行尝试右边。
如果都不行,做merge。
比如删除30,造成29替换30,剩下28,28左边兄弟key数不够,右边又没有兄弟。要对28这个节点做merge。

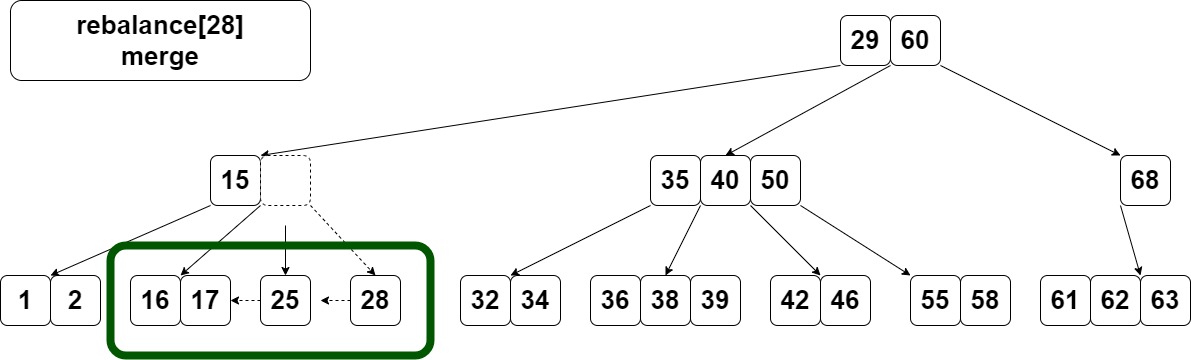
merge分不分左右?写代码时会发现可以处理一下,只写一个方向的就行。
把25拉下来接到左边兄弟最后,把节点n所有节点再接到它最后,变成[16,17,25,28],父节点变成[15]。
这时父节点的这个key没了,节点n也空了。可把n删除。
merge后的节点key数一定不会超标。 因为左边兄弟最多t-1,否则直接拿过来就行。本身必然是t-2,否则不用走rebalance。再加上拉下来的1,结果是t-1+t-2+1=2t-2。
这时要检查父节点key数,因为被拉下去一个key。
如果父节点不是根
如果剩余key数大于等于t-1。成功返回。
否则走rebalance(父节点)。
如果父节点是根
如果剩余key数大于0。成功返回。
否则父节点唯一的key被拉下来merge到了新节点。把这个新节点作为新的根即可。

如图,如果红色节点存在,merge即可,根还有一个key60。 如果红色节点不存在,merge时把29拉下来造成根节点为空。那么直接让merge出来的节点成为根即可。
子树问题
rebalance走到内部节点时要考虑子树问题。这个很多资料没有说明。 比如现在父节点只有一个15了。rebalance发现右边兄弟有3个key,按说是逆时针旋转29和35,但是35的左子树怎么办? 看下35的子树区间,强行替换后35的左子树区间为[29, 35],发现如果旋转后把35的左子树变成29的右子树刚好能解决问题。
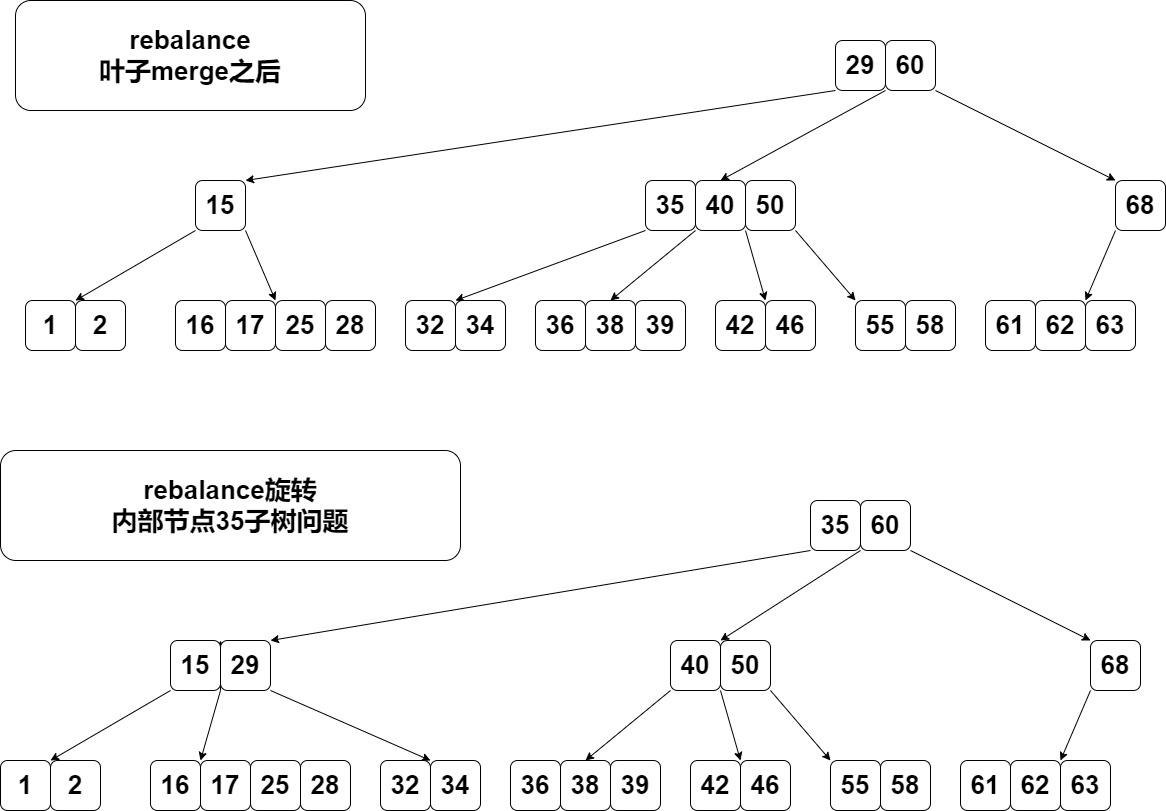
如图。29转下来,35转上去,35的左子树变成29的右子树。
内部节点merge不需要处理子树,merge完判断一下是否要rebalance父节点即可。
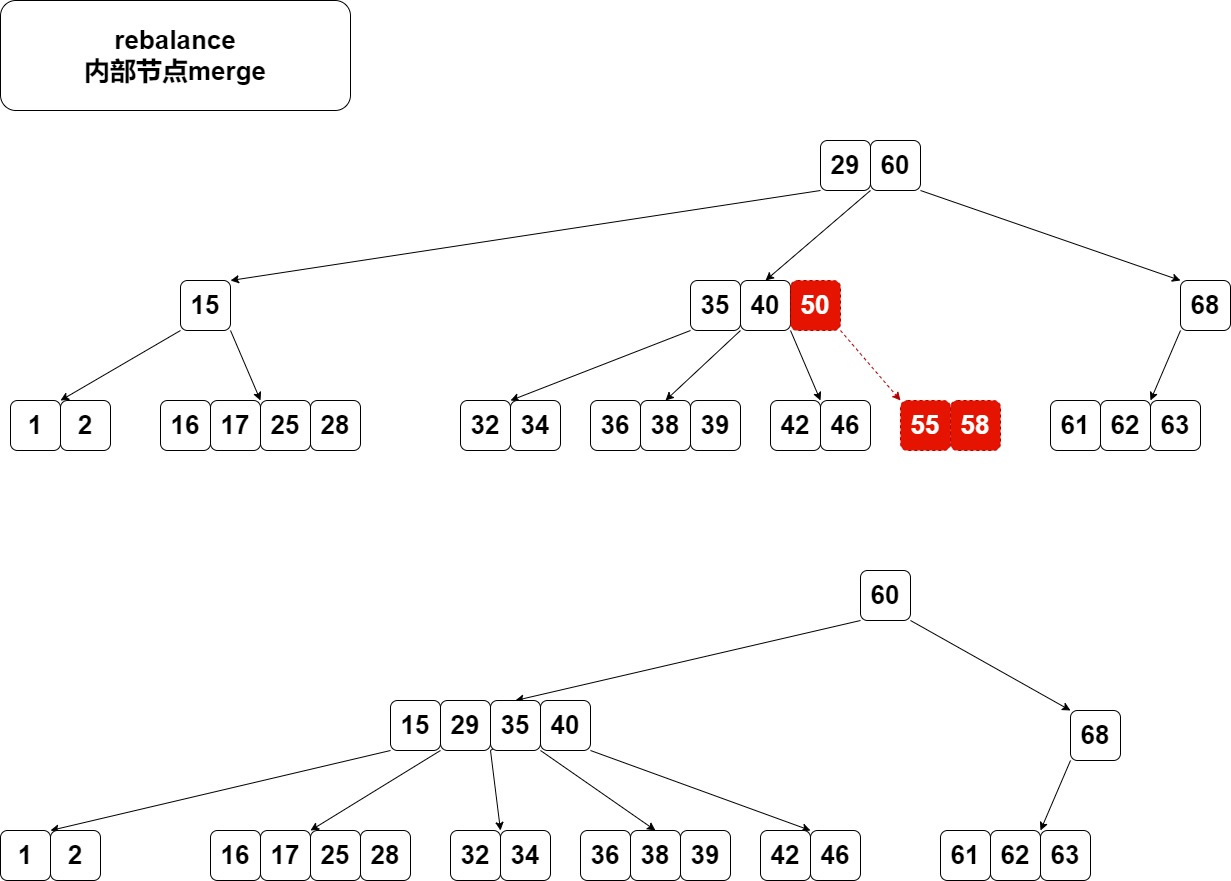
如图,如果红色节点不存在,进行merge,不需要处理子树。
测试#
测试其实很有讲究。这里没能力去总结。只做简单测试,尽量保证逻辑正确。并记录一下平均操作耗时。
确定数据量比如100000个随机数。依次插入。
随机搜索插入过的、未插入过的数,看是否找的到。
随机删除插入过的、未插入过的数。再搜索。
检测数据总量是否正确。可做一一对比。
删除所有数据并检查。
发挥想象
记录所有操作的耗时。观察内存占用。 这里简单测试,不再做图。 插入的总key数100万。 md递增,从2到1000。
CPU是intel i5 6600k 3.5GHz
Btree PrintInfo:
md = 2
total_nodes = 1000000
height = 16
test_0_result avg time 10131 nanoseconds 插入所有
test_1_result avg time 6340 nanoseconds 查询所有
test_2_result avg time 6668 nanoseconds 查询不存在的
test_3_result avg time 8100 nanoseconds 插入已存在的
test_4_result avg time 11432 nanoseconds 删除存在的
test_5_result avg time 7524 nanoseconds 查询被删除的
test_6_result avg time 7073 nanoseconds 查询没被删除的
test_7_result avg time 4175 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 11172 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 10539 nanoseconds 插入所有
test_12_result avg time 300 nanoseconds 查询节点数
Btree PrintInfo:
md = 5
total_nodes = 1000000
height = 8
test_0_result avg time 4792 nanoseconds 插入所有
test_1_result avg time 3475 nanoseconds 查询所有
test_2_result avg time 3617 nanoseconds 查询不存在的
test_3_result avg time 3607 nanoseconds 插入已存在的
test_4_result avg time 4780 nanoseconds 删除存在的
test_5_result avg time 3653 nanoseconds 查询被删除的
test_6_result avg time 3494 nanoseconds 查询没被删除的
test_7_result avg time 2734 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 5182 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 4876 nanoseconds 插入所有
test_12_result avg time 200 nanoseconds 查询节点数
Btree PrintInfo:
md = 10
total_nodes = 1000000
height = 6
test_0_result avg time 3707 nanoseconds 插入所有
test_1_result avg time 2853 nanoseconds 查询所有
test_2_result avg time 3019 nanoseconds 查询不存在的
test_3_result avg time 2710 nanoseconds 插入已存在的
test_4_result avg time 3773 nanoseconds 删除存在的
test_5_result avg time 2897 nanoseconds 查询被删除的
test_6_result avg time 2778 nanoseconds 查询没被删除的
test_7_result avg time 2296 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 4069 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 3614 nanoseconds 插入所有
test_12_result avg time 200 nanoseconds 查询节点数
Btree PrintInfo:
md = 20
total_nodes = 1000000
height = 5
test_0_result avg time 3267 nanoseconds 插入所有
test_1_result avg time 2399 nanoseconds 查询所有
test_2_result avg time 2471 nanoseconds 查询不存在的
test_3_result avg time 2241 nanoseconds 插入已存在的
test_4_result avg time 3648 nanoseconds 删除存在的
test_5_result avg time 2481 nanoseconds 查询被删除的
test_6_result avg time 2385 nanoseconds 查询没被删除的
test_7_result avg time 2016 nanoseconds 删除不存在的
test_8_result avg time 500 nanoseconds 查询节点数
test_9_result avg time 3906 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 3344 nanoseconds 插入所有
test_12_result avg time 200 nanoseconds 查询节点数
Btree PrintInfo:
md = 50
total_nodes = 1000000
height = 4
test_0_result avg time 3731 nanoseconds 插入所有
test_1_result avg time 2115 nanoseconds 查询所有
test_2_result avg time 2207 nanoseconds 查询不存在的
test_3_result avg time 1888 nanoseconds 插入已存在的
test_4_result avg time 4377 nanoseconds 删除存在的
test_5_result avg time 2180 nanoseconds 查询被删除的
test_6_result avg time 2102 nanoseconds 查询没被删除的
test_7_result avg time 1828 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 4679 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 3700 nanoseconds 插入所有
test_12_result avg time 300 nanoseconds 查询节点数
Btree PrintInfo:
md = 100
total_nodes = 1000000
height = 3
test_0_result avg time 4970 nanoseconds 插入所有
test_1_result avg time 1866 nanoseconds 查询所有
test_2_result avg time 1961 nanoseconds 查询不存在的
test_3_result avg time 1561 nanoseconds 插入已存在的
test_4_result avg time 5915 nanoseconds 删除存在的
test_5_result avg time 1989 nanoseconds 查询被删除的
test_6_result avg time 1849 nanoseconds 查询没被删除的
test_7_result avg time 1646 nanoseconds 删除不存在的
test_8_result avg time 300 nanoseconds 查询节点数
test_9_result avg time 6458 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 4891 nanoseconds 插入所有
test_12_result avg time 300 nanoseconds 查询节点数
Btree PrintInfo:
md = 200
total_nodes = 1000000
height = 3
test_0_result avg time 7941 nanoseconds 插入所有
test_1_result avg time 1867 nanoseconds 查询所有
test_2_result avg time 1986 nanoseconds 查询不存在的
test_3_result avg time 1577 nanoseconds 插入已存在的
test_4_result avg time 9201 nanoseconds 删除存在的
test_5_result avg time 1956 nanoseconds 查询被删除的
test_6_result avg time 1855 nanoseconds 查询没被删除的
test_7_result avg time 1630 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 10544 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 7712 nanoseconds 插入所有
test_12_result avg time 300 nanoseconds 查询节点数
Btree PrintInfo:
md = 500
total_nodes = 1000000
height = 3
test_0_result avg time 16252 nanoseconds 插入所有
test_1_result avg time 1795 nanoseconds 查询所有
test_2_result avg time 1895 nanoseconds 查询不存在的
test_3_result avg time 1531 nanoseconds 插入已存在的
test_4_result avg time 24504 nanoseconds 删除存在的
test_5_result avg time 1879 nanoseconds 查询被删除的
test_6_result avg time 1789 nanoseconds 查询没被删除的
test_7_result avg time 1572 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 22461 nanoseconds 删除所有
test_10_result avg time 200 nanoseconds 查询节点数
test_11_result avg time 16335 nanoseconds 插入所有
test_12_result avg time 300 nanoseconds 查询节点数
Btree PrintInfo:
md = 1000
total_nodes = 1000000
height = 2
test_0_result avg time 30469 nanoseconds 插入所有
test_1_result avg time 1645 nanoseconds 查询所有
test_2_result avg time 1748 nanoseconds 查询不存在的
test_3_result avg time 1286 nanoseconds 插入已存在的
test_4_result avg time 49086 nanoseconds 删除存在的
test_5_result avg time 1744 nanoseconds 查询被删除的
test_6_result avg time 1637 nanoseconds 查询没被删除的
test_7_result avg time 1444 nanoseconds 删除不存在的
test_8_result avg time 200 nanoseconds 查询节点数
test_9_result avg time 42441 nanoseconds 删除所有
test_10_result avg time 300 nanoseconds 查询节点数
test_11_result avg time 30501 nanoseconds 插入所有
test_12_result avg time 200 nanoseconds 查询节点数
可以看到随md增大,插入时间从大变小再变大。
变小是因为md越大,树高度越小。是在较大空间内进行少数几次二分查找,而不在较小的空间内进行多次二分查找。每次深入子节点都是换空间,读的实际内存和磁盘可能根之前空间有距离。我们目前的数据应该用不到磁盘,但是原理是一样的,实用时进入子树可能会读一大块磁盘数据。
后来又变慢,是因为节点存key用的vector数组,插入后需要把插入点之后的所有数据更新一遍,量大时效率很低。
随md增大,查询是越来越快。因为空间转换次数变少,且在数组的连续空间里,key在1000这个级别,二分查找很快。
随md增大,插入已存在的也是越来越快,因为已存在,不用插入,相当于查找。
随md增大,删除是先变快再变慢。原因和插入类似。
总结#
wikipedia的删除操作讲的比较清晰
优化问题 有的操作可以省略,比如删除再rebalance。删除时会移动大批数据,rebalance时又可能会填进去,造成重复劳动。 vector问题。插入头部效率低,需要移动所有数据。 我的代码是很朴素的实现,没有处理这些问题。
整个算法还是相对容易。对着流程和图示调试就行。需要注意各种边界,注意数据改变时的更新,很容易漏更新。
做一个打印整棵树的函数。非常香。
调试数据做100个key多试几次,基本可以覆盖所有错误情况。
如果树很大,调试也不用看全部的节点,只需看小范围节点,基本跟踪个一两层就能发现问题。
参考#
https://en.wikipedia.org/wiki/B-tree <<算法导论>> https://cstack.github.io/db_tutorial/ https://www.programiz.com/dsa/b-tree https://dzone.com/articles/database-btree-indexing-in-sqlite https://scanftree.com/Data_Structure/deletion-in-b-tree https://www.cs.yale.edu/homes/aspnes/pinewiki/BTrees.html https://www.geeksforgeeks.org/introduction-of-b-tree-2/ https://www.codercto.com/a/83791.html https://www.cs.cornell.edu/courses/cs3110/2012sp/recitations/rec25-B-trees/rec25.html https://github.com/google/btree
代码#
BTree.h
// btree
// 20210216 xc
#pragma once
#include <iostream>
#include <memory>
#include <vector>
#include <deque>
#include <tuple>
#include <cassert>
class BTreeNode
{
friend class BTree;
std::vector<int> keys;
std::vector<std::shared_ptr<BTreeNode>> children;
//std::deque<int> keys;
//std::deque<std::shared_ptr<BTreeNode>> children;
std::shared_ptr<BTreeNode> pnt;
bool is_leaf;
int key_count; // key_count == keys.size()
int pnt_pos; // parent's children index. pnt->children[pnt_pos] == me
public:
BTreeNode();
BTreeNode(std::shared_ptr<BTreeNode> n, int i);
};
BTreeNode::BTreeNode():keys(0), children(0)
{
this->key_count = 0;
this->is_leaf = true;
this->pnt = nullptr;
this->pnt_pos = 0;
}
BTreeNode::BTreeNode(std::shared_ptr<BTreeNode> n, int pos)
{
// copy data from pos to new node
this->key_count = n->key_count / 2;
this->is_leaf = n->is_leaf;
this->pnt_pos = n->pnt_pos;
this->keys = std::vector<int>(this->key_count);
//this->keys = std::deque<int>(this->key_count);
for (int i = 0, j = n->key_count / 2 + 1; i < this->key_count; ++i, ++j)
this->keys[i] = n->keys[j];
if (!n->is_leaf)
{
this->children = std::vector<std::shared_ptr<BTreeNode>>(this->key_count + 1, nullptr);
//this->children = std::deque<std::shared_ptr<BTreeNode>>(this->key_count + 1, nullptr);
for (int i = 0, j = n->key_count / 2 + 1; i <= this->key_count; ++i, ++j)
{
this->children[i] = n->children[j];
this->children[i]->pnt_pos = i;
}
}
}
class BTree
{
private:
std::shared_ptr<BTreeNode> root;
int md; // minimum degree
int height;
int total_keys;
int total_nodes;
int SplitChild(std::shared_ptr<BTreeNode> n, int i);
int InsertNonFull(std::shared_ptr<BTreeNode> n, int key);
std::tuple<int, std::shared_ptr<BTreeNode>, int> SearchKey(std::shared_ptr<BTreeNode> n, int key);
int Rebalance(std::shared_ptr<BTreeNode> n);
int Destroy(std::shared_ptr<BTreeNode> n);
void PrintNode(std::shared_ptr<BTreeNode> n, int level);
public:
int PrintInfo();
int Insert(int key);
int Find(int key);
int Delete(int key);
int TotalNodes();
int TotalKeys();
void PrintTree();
BTree();
BTree(int md);
~BTree();
};
BTree::BTree()
{
std::cout << "Btree born" << std::endl;
}
BTree::~BTree()
{
std::cout << "Btree die" << std::endl;
this->Destroy(this->root);
}
BTree::BTree(int md)
{
std::cout << "Btree born" << std::endl;
this->md = md;
this->height = 1;
this->total_keys = 0;
this->total_nodes = 1;
root = std::make_shared<BTreeNode>();
}
void BTree::PrintNode(std::shared_ptr<BTreeNode> n, int level)
{
if(n->is_leaf)
std::cout << "leaf-";
std::cout << "[count "<<n->key_count<<"][pnt_pos "<<n->pnt_pos <<"]node=";
for (int i = 0; i < n->keys.size(); ++i)
{
std::cout << n->keys[i] << "-";
}
std::cout << std::endl;
if (n->is_leaf)
return;
for (int i = 0; i < n->children.size(); ++i)
{
for (int i = 0; i < level * 8; ++i)
std::cout << " ";
std::cout << "child-" << i <<"-";
assert(n->children[i]->pnt == n);
PrintNode(n->children[i], level + 1);
}
}
void BTree::PrintTree()
{
PrintInfo();
PrintNode(this->root, 1);
}
int BTree::SplitChild(std::shared_ptr<BTreeNode> n, int pos) // 分裂index为i-1和i之间的子节点。子节点一定是满的才分裂。
{
//std::cout << "SplitChild" << std::endl;
auto cn = n->children[pos];
auto new_right = std::make_shared<BTreeNode>(cn, cn->key_count / 2 + 1);
new_right->pnt = n;
new_right->pnt_pos ++;
// insert into n
n->keys.resize(n->keys.size() + 1);
n->children.resize(n->children.size() + 1);
for (int j = n->key_count; j > pos; --j) // 效率低
{
n->keys[j] = n->keys[j - 1]; // move forward
n->children[j + 1] = n->children[j]; // move forward
}
n->keys[pos] = cn->keys[cn->key_count / 2];
n->children[pos + 1] = new_right;
cn->keys.resize(cn->key_count / 2);
cn->children.resize(cn->key_count / 2 + 1);
cn->key_count /= 2;
n->key_count++;
// update pnt
if(!new_right->is_leaf)
for (int i = 0; i <= new_right->key_count; ++i)
new_right->children[i]->pnt = new_right;
this->total_nodes++;
return 0;
}
int BTree::InsertNonFull(std::shared_ptr<BTreeNode> n, int key)
{
if (n->key_count == 0 && n->is_leaf)
{
n->keys.push_back(key);
n->key_count++;
return 0;
}
// binary search
int i = 0, j = n->key_count - 1, pos = 0, temp_key = 0;
for (;;)
{
if (i == j) // 2 slots
{
if (n->keys[i] == key)
return 1;
if (n->keys[i] > key)
pos = i;
else
pos = i + 1;
break;
}
if (i + 1 == j) // 3 slots
{
if (n->keys[i] == key || n->keys[j] == key)
return 1; // exists
if (n->keys[i] > key)
pos = i;
else if (n->keys[j] < key)
pos = j + 1;
else
pos = j;
break;
}
pos = (i + j) / 2;
temp_key = n->keys[pos];
if (temp_key == key)
return 1; // exists
if (temp_key > key)
j = pos;
else
i = pos;
}
if (n->is_leaf)
{
n->keys.resize(n->key_count + 1);
for (int i = n->key_count; i > pos; --i) // 效率低
n->keys[i] = n->keys[i - 1]; // move forward
n->key_count++;
n->keys[pos] = key;
return 0;
}
else
{
auto cn = n->children[pos];
if (cn->key_count >= this->md * 2 - 1)
{
auto result = SplitChild(n, pos);
// update pnt_pos
for (int i = pos + 2; i <= n->key_count; ++i)
n->children[i]->pnt_pos = i;
// check the center key
if (n->keys[pos] == key)
return 1;
if (n->keys[pos] < key)
++pos;
}
return InsertNonFull(n->children[pos], key);
}
}
int BTree::Insert(int key)
{
//std::cout << "Insert "<< key << std::endl;
if (this->root->key_count >= this->md * 2 - 1) // root is full
{
//std::cout << "Insert new_root" << std::endl;
auto new_root = std::make_shared<BTreeNode>();
new_root->is_leaf = false;
new_root->children.push_back(this->root);
this->root->pnt = new_root;
this->root->pnt_pos = 0;
this->root = new_root;
this->total_nodes++;
SplitChild(this->root, 0);
this->height++;
//PrintTree();
}
auto result = InsertNonFull(this->root, key);
if (result == 0)
{
this->total_keys++;
}
//PrintTree();
return result;
}
int BTree::Find(int key)
{
//PrintTree();
int result, pos;
std::shared_ptr<BTreeNode> node;
std::tie(result, node, pos) = SearchKey(this->root, key);
return result;
}
int BTree::TotalKeys()
{
return this->total_keys;
}
int BTree::TotalNodes()
{
return this->total_nodes;
}
std::tuple<int, std::shared_ptr<BTreeNode>, int> BTree::SearchKey(std::shared_ptr<BTreeNode> n, int key)
{
//std::cout << "Search "<<key << std::endl;
if (n->key_count == 0) // fail
return std::tuple<int, std::shared_ptr<BTreeNode>, int>(0, nullptr, 0);
// binary seatch
int i = 0, j = n->key_count - 1, pos = 0, temp_key = 0;
for (;;)
{
if (i == j)
{
if (n->keys[i] == key)
return std::tuple<int, std::shared_ptr<BTreeNode>, int>(1, n, i);
if (n->keys[i] > key)
pos = i;
else
pos = i + 1;
break;
}
if (i + 1 == j)
{
if (n->keys[i] == key)
return std::tuple<int, std::shared_ptr<BTreeNode>, int>(1, n, i);
if (n->keys[j] == key)
return std::tuple<int, std::shared_ptr<BTreeNode>, int>(1, n, j);
if (n->keys[i] > key)
pos = i;
else if (n->keys[j] < key)
pos = j + 1;
else
pos = j;
break;
}
pos = (i + j) / 2;
temp_key = n->keys[pos];
if (temp_key == key)
return std::tuple<int, std::shared_ptr<BTreeNode>, int>(1, n, pos);
if (temp_key > key)
j = pos;
else
i = pos;
}
if (n->is_leaf) // fail
return std::tuple<int, std::shared_ptr<BTreeNode>, int>(0, nullptr, 0);
else
return SearchKey(n->children[pos], key);
}
int BTree::Delete(int key)
{
//std::cout << "!!!!!!!!!!!!!!!!!Delete "<< key << std::endl;
//PrintTree();
int result, pos;
std::shared_ptr<BTreeNode> n;
std::tie(result, n, pos) = SearchKey(this->root, key);
if (result == 0) // not found
return 1;
if (n->is_leaf)
{
for (int i = pos; i < n->key_count - 1; ++i)
{
n->keys[i] = n->keys[i + 1];
}
n->keys.pop_back();
n->key_count--;
if (n->key_count >= (this->md - 1) || this->root == n)
{
this->total_keys--;
return 0;
}
auto result = Rebalance(n);
if (result == 0) // ok
{
this->total_keys--;
return 0;
}
else
{
return result;
}
}
else
{
// search left subtree
auto left_node = n->children[pos];
for (;;)
{
if (left_node->is_leaf)
break;
left_node = left_node->children.back();
}
if (left_node->key_count >= this->md) // can grab
{
n->keys[pos] = left_node->keys.back(); // replace key
left_node->keys.pop_back();
left_node->key_count--;
this->total_keys--;
return 0;
}
// search right subtree
auto right_node = n->children[pos + 1];
for (;;)
{
if (right_node->is_leaf)
break;
right_node = right_node->children.front();
}
if (right_node->key_count >= this->md) // can grab
{
n->keys[pos] = right_node->keys.front(); // replace key
for (int i = 0; i < right_node->key_count - 1; ++i)
right_node->keys[i] = right_node->keys[i + 1]; // move backward
right_node->key_count--;
right_node->keys.pop_back();
this->total_keys--;
return 0;
}
// all fail. force replace with left.
n->keys[pos] = left_node->keys.back(); // replace key
left_node->keys.pop_back();
left_node->key_count--;
//PrintTree();
auto result = Rebalance(left_node);
if (result == 0)
{
this->total_keys--;
return 0;
}
else
{
return result;
}
}
}
int BTree::Rebalance(std::shared_ptr<BTreeNode> n)
{
//std::cout << "Rebalance " << std::endl;
//PrintTree();
// check left bro
if (n->pnt_pos > 0) // has left bro
{
auto left_bro = n->pnt->children[n->pnt_pos - 1];
//std::cout << "check left bro. key_count = "<< left_bro->key_count << std::endl;
if (left_bro->key_count >= this->md)
{
// parent rotate down
n->keys.push_back(0);
n->key_count++;
for (int i = n->key_count - 1; i >= 1; --i) // move all keys
n->keys[i] = n->keys[i - 1];
n->keys[0] = n->pnt->keys[n->pnt_pos - 1];
if (!n->is_leaf)
{
n->children.push_back(nullptr);
for (int i = n->key_count; i >= 1; --i) // move all children
{
n->children[i] = n->children[i - 1];
n->children[i]->pnt_pos++;
}
// take left bro's subtree
n->children[0] = left_bro->children.back();
n->children[0]->pnt = n;
n->children[0]->pnt_pos = 0;
left_bro->children.pop_back();
}
n->pnt->keys[n->pnt_pos - 1] = left_bro->keys.back(); // left bro's last key rotate up
// delete right bro's last key
left_bro->keys.pop_back();
left_bro->key_count--;
return 0;
}
}
// check right bro
if (n->pnt_pos < n->pnt->key_count) // has right bro
{
auto right_bro = n->pnt->children[n->pnt_pos + 1];
//std::cout << "check right bro. key_count = " << right_bro->key_count << std::endl;
if (right_bro->key_count >= this->md)
{
n->keys.push_back(n->pnt->keys[n->pnt_pos]); // parent rotate down
n->key_count++;
if (!n->is_leaf)
{
// take right bro's subtree
n->children.push_back(right_bro->children.front());
n->children.back()->pnt_pos = n->key_count;
n->children.back()->pnt = n;
}
n->pnt->keys[n->pnt_pos] = right_bro->keys.front(); // right bro's first key rotate up
// delete right bro's first key
for (int i = 0; i < right_bro->key_count - 1; ++i)
right_bro->keys[i] = right_bro->keys[i + 1];
if (!n->is_leaf)
{
for (int i = 0; i <= right_bro->key_count - 1; ++i)
{
right_bro->children[i] = right_bro->children[i + 1];
right_bro->children[i]->pnt_pos--;
}
right_bro->children.pop_back();
}
right_bro->keys.pop_back();
right_bro->key_count--;
return 0;
}
}
// all bro fail. do merge.
// set left
auto left = n;
if (n->pnt_pos > 0) // has left bro
left = n->pnt->children[n->pnt_pos - 1];
auto right = left->pnt->children[left->pnt_pos + 1];
//std:: cout<< "left key 0 " << left->keys[0] << " righ " << right->keys[0] << std::endl;
// update right children pnt_pos
if (!right->is_leaf)
{
for (int i = 0; i <= right->key_count; ++i)
{
right->children[i]->pnt_pos += left->key_count + 1;
right->children[i]->pnt = left;
}
}
left->keys.push_back(left->pnt->keys[left->pnt_pos]); // push parent key
left->keys.insert(left->keys.end(), right->keys.begin(), right->keys.end()); // push back right keys
if (!right->is_leaf)
left->children.insert(left->children.end(), right->children.begin(), right->children.end()); // push back right children
left->key_count += right->key_count + 1;
// move parent key and children
for (int i = left->pnt_pos; i < left->pnt->key_count - 1; ++i)
left->pnt->keys[i] = left->pnt->keys[i + 1];
for (int i = left->pnt_pos + 1; i <= left->pnt->key_count - 1; ++i)
{
left->pnt->children[i] = left->pnt->children[i + 1];
left->pnt->children[i]->pnt_pos = i;
}
left->pnt->keys.pop_back();
left->pnt->children.pop_back();
left->pnt->key_count--;
this->total_nodes--;
if (left->pnt == this->root)
{
if (left->pnt->key_count > 0)
return 0;
// root empty
this->root = left;
this->height--;
this->total_nodes--;
return 0;
}
if (left->pnt->key_count >= this->md - 1)
return 0;
return Rebalance(left->pnt);
}
int BTree::Destroy(std::shared_ptr<BTreeNode> n)
{
return 0;
}
int BTree::PrintInfo()
{
std::cout << "Btree PrintInfo:" << std::endl;
std::cout << "md = "<< this->md << std::endl;
std::cout << "total_keys = " << this->total_keys << std::endl;
std::cout << "total_nodes = " << this->total_nodes << std::endl;
std::cout << "height = " << this->height << std::endl;
return 0;
}
BTree.cpp
#include <iostream>
#include <fstream>
#include <chrono>
#include <cassert>
#include <memory>
#include "BTree.h"
int total_nodes, md, gap;
int test_case(std::shared_ptr<BTree> btree, int task, int answer, std::fstream &fs)
{
// insert_all
long long total_time = 0;
int count = 0;
int data = 0;
for (;;)
{
fs >> data;
if (data == gap)
break;
auto t1 = std::chrono::system_clock::now();
int result = -1;
switch (task)
{
case 0:
result = btree->Insert(data);
break;
case 1:
result = btree->Find(data);
break;
case 2:
result = btree->Find(data);
break;
case 3:
result = btree->Insert(data);
break;
case 4:
//std::cout << "delete " << data << std::endl;
//btree->PrintTree();
result = btree->Delete(data);
break;
case 5:
result = btree->Find(data);
break;
case 6:
result = btree->Find(data);
break;
case 7:
//std::cout << "delete " << data << std::endl;
//btree->PrintTree();
result = btree->Delete(data);
break;
case 8:
answer = data;
result = btree->TotalKeys();
break;
case 9:
//std::cout << "delete " << data << std::endl;
//btree->PrintTree();
result = btree->Delete(data);
break;
case 10:
answer = data;
result = btree->TotalKeys();
break;
case 11:
result = btree->Insert(data);
break;
case 12:
answer = data;
result = btree->TotalKeys();
break;
}
if (answer != -1) // don't need to check
{
if (result != answer)
std::cerr << "task " << task << " failed " << data << std::endl;
assert(result == answer);
}
auto t2 = std::chrono::system_clock::now();
auto nanoseconds = std::chrono::duration_cast<std::chrono::nanoseconds>(t2 - t1).count(); // microseconds nanoseconds
total_time += nanoseconds;
//std::cout << "milliseconds " << milliseconds << std::endl;
count++;
}
switch (task)
{
case 0:
std::cout << "insert all nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 1:
std::cout << "find all good nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 2:
std::cout << "find all bad nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 3:
std::cout << "insert dup nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 4:
std::cout << "delete nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 5:
std::cout << "find deleted nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 6:
std::cout << "find not deleted nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 7:
std::cout << "deleted not exist nodes ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 8:
std::cout << "check size ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 9:
std::cout << "delete all ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 10:
std::cout << "check size ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 11:
std::cout << "insert all ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
case 12:
std::cout << "check size ok avg time = " << total_time / count << " nanoseconds" << std::endl;
break;
}
return total_time / count;
}
int simple_test()
{
//auto t0 = std::time(nullptr);
std::fstream fs("btree_test_data_1.txt", std::fstream::in);
if (!fs.is_open())
{
std::cout << "no test data\n";
return 1;
}
fs >> total_nodes >>md >> gap;
std::cout << md <<" "<<total_nodes<<" "<< gap <<std::endl;
auto btree = std::make_shared<BTree>(md);
//btree->PrintInfo();
auto test_0_result = test_case(btree, 0, 0, fs);
//btree->PrintInfo();
auto test_1_result = test_case(btree, 1, 1, fs);
auto test_2_result = test_case(btree, 2, 0, fs);
auto test_3_result = test_case(btree, 3, 1, fs);
//btree->PrintTree();
auto test_4_result = test_case(btree, 4, 0, fs);
//btree->PrintTree();
auto test_5_result = test_case(btree, 5, 0, fs);
//btree->PrintTree();
auto test_6_result = test_case(btree, 6, 1, fs);
auto test_7_result = test_case(btree, 7, 1, fs);
//btree->PrintTree();
btree->PrintInfo();
auto test_8_result = test_case(btree, 8, 0, fs);
btree->PrintInfo();
auto test_9_result = test_case(btree, 9, -1, fs);
//btree->PrintTree();
btree->PrintInfo();
auto test_10_result = test_case(btree, 10, 0, fs);
auto test_11_result = test_case(btree, 11, 0, fs);
auto test_12_result = test_case(btree, 12, 0, fs);
btree->PrintInfo();
std::cout << "test_0_result avg time " << test_0_result << " nanoseconds" << std::endl
<< "test_1_result avg time " << test_1_result << " nanoseconds" << std::endl
<< "test_2_result avg time " << test_2_result << " nanoseconds" << std::endl
<< "test_3_result avg time " << test_3_result << " nanoseconds" << std::endl
<< "test_4_result avg time " << test_4_result << " nanoseconds" << std::endl
<< "test_5_result avg time " << test_5_result << " nanoseconds" << std::endl
<< "test_6_result avg time " << test_6_result << " nanoseconds" << std::endl
<< "test_7_result avg time " << test_7_result << " nanoseconds" << std::endl
<< "test_8_result avg time " << test_8_result << " nanoseconds" << std::endl
<< "test_9_result avg time " << test_9_result << " nanoseconds" << std::endl
<< "test_10_result avg time " << test_10_result << " nanoseconds" << std::endl
<< "test_11_result avg time " << test_11_result << " nanoseconds" << std::endl
<< "test_12_result avg time " << test_12_result << " nanoseconds" << std::endl;
return 0;
}
int main()
{
simple_test();
return 0;
}
python生成测试数据
import random
TOTAL_SIZE = 100
MINIMUM_ORDER = 3
MAX_VALUE = 1000
FIND_FAIL_COUNT = 20
DELETE_OK_COUNT = 20
TOTAL_SIZE = 1000000
MINIMUM_ORDER = 20
MAX_VALUE = 10000000
FIND_FAIL_COUNT = 100000
DELETE_OK_COUNT = 100000
TOTAL_SIZE = 1000
MINIMUM_ORDER = 3
MAX_VALUE = 10000
FIND_FAIL_COUNT = 500
DELETE_OK_COUNT = 500
TOTAL_SIZE = 10000
MINIMUM_ORDER = 10
MAX_VALUE = 100000
FIND_FAIL_COUNT = 500
DELETE_OK_COUNT = 200
TOTAL_SIZE = 100000
MINIMUM_ORDER = 10
MAX_VALUE = 10000000
FIND_FAIL_COUNT = 500
DELETE_OK_COUNT = 200
GAP = -999999999
'''
TOTAL_SIZE
insert ok data
find ok data
find fail data
insert dup data
delete exist
find deleted
find not deleted
delete not exist
check size TOTAL_SIZE - DELETE_OK_COUNT
delete all
check size 0
'''
def gen_data():
good_data_set = set()
#find_ok_data_set = set()
count = 0
dup_data = set()
delete_data_list = []
no_delete_data_list = []
with open("btree_test_data_2.txt", 'w') as f:
f.write("%d\n%d\n%d\n" % (TOTAL_SIZE, MINIMUM_ORDER, GAP))
while(True):
data = random.randint(0, MAX_VALUE)
if data not in good_data_set:
f.write("%d\n" % data)
good_data_set.add(data)
count += 1
if count >= TOTAL_SIZE:
f.write("%d\n" % GAP)#f.write("INSERT_OVER\n")
break
else:
dup_data.add(data)
# find all ok
good_data_list = list(good_data_set)
random.shuffle(good_data_list)
for data in good_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP)#f.write("FIND_OK_OVER\n")
# find all fail
count = 0
while (True):
data = random.randint(0, MAX_VALUE)
if data not in good_data_set:
f.write("%d\n" % data)
count += 1
if count == FIND_FAIL_COUNT:
break
f.write("%d\n" % GAP)#f.write("FIND_FAIL_OVER\n")
# dup all
random.shuffle(good_data_list)
for data in good_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP)#f.write("INSERT_DUP_OVER\n")
# delete ok
count = 0
random.shuffle(good_data_list)
delete_data_list = good_data_list[:DELETE_OK_COUNT]
no_delete_data_list = good_data_list[DELETE_OK_COUNT:]
for data in delete_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP) # f.write("INSERT_DUP_OVER\n")
# find deleted
count = 0
random.shuffle(delete_data_list)
for data in delete_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP) # f.write("INSERT_DUP_OVER\n")
# find not deleted
for data in no_delete_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP) # f.write("INSERT_DUP_OVER\n")
# delete not exist
count = 0
while (True):
data = random.randint(0, MAX_VALUE * 10)
if data not in good_data_set:
f.write("%d\n" % data)
count += 1
if count == DELETE_OK_COUNT:
break
f.write("%d\n" % GAP) # f.write("FIND_FAIL_OVER\n")
f.write("%d\n" % (TOTAL_SIZE - DELETE_OK_COUNT))
f.write("%d\n" % GAP)
# delete all
random.shuffle(good_data_list)
for data in good_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP)
# check size
f.write("%d\n" % 0)
f.write("%d\n" % GAP)
# insert all
random.shuffle(good_data_list)
for data in good_data_list:
f.write("%d\n" % data)
f.write("%d\n" % GAP)
# check size
f.write("%d\n" % TOTAL_SIZE)
f.write("%d\n" % GAP)
gen_data()